Two identical wires $A and B$ , each of length 'l', carry the same current $I$ . Wire A is bent into a circle of radius $R and w i r e B$ is bent to form a square of side 'a' . If $B_{A} and B_{B}$ are the values of magnetic field at the centres of the circle and square respectively , then the ratio $\frac{B_{A}}{B_{B}}$ is :

A

$\frac{π^{2}}{8}$

B

$\frac{π^{2}}{16 \sqrt{2}}$

C

$\frac{π^{2}}{16}$

D

$\frac{π^{2}}{8 \sqrt{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:b

Let r be the radius of circle formed then we can write $l = 2 π r \Rightarrow r = l / 2 π$
Magnetic field at the centre of circle
$B_{A} = \frac{μ_{0} I}{2 r} = \frac{μ_{0} I}{2 \times \frac{l}{2 π}} = \frac{μ_{0} π I}{l}$

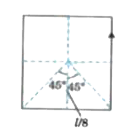
There are four sides hence magnetic field due to one side is multiplied to four.
$B_{B} = 4 \times \frac{μ_{0} I}{2 π \frac{l}{8}} (sin 45 + sin 45) = \frac{16 μ_{0} I \sqrt{2}}{π l}$
$\frac{B_{A}}{B_{B}} = \frac{\frac{μ_{0} π I}{l}}{\frac{16 μ_{0} I \sqrt{2}}{π l}} = \frac{π^{2}}{16 \sqrt{2}}$
Thus, option (b) is correct.

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two identical wires A and B have the same length l and carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side a. If $B_{1} and B_{2}$ are the values of magnetic induction at the centre of the circle and the centre of the square, respectively, then the ratio $B_{1} / B_{2}$ is
A $(π^{2} / 8)$
B $(π^{2} / 8 \sqrt{2})$
C $(π^{2} / 16)$
D $(π^{2} / 16 \sqrt{2})$
Question 2 - Select One
Two identical wires A and B have the same length L and carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side a. If $B_{1} and B_{2}$ are the values of magnetic induction at the centre of the square respectively, then the ratio is $\frac{B_{1}}{B_{2}}$ is
A $(\frac{π^{2}}{8})$
B $(\frac{π^{2}}{8 \sqrt{2}})$
C $(\frac{π^{2}}{16})$
D $(\frac{π^{2}}{16 \sqrt{2}})$
Question 3 - Select One
A wire of length l, carrying current i, is bent in circle of radius r, then magnetic momennt at centre of loop is
A $\frac{l^{2} i}{2 π}$
B $\frac{l^{2} i}{4 π}$
C $\frac{l i^{2}}{2 π}$
D $\frac{l i}{4 π}$

MODERN PUBLICATION-MOVING CHARGES AND MAGNETISM-COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)

Home
Ask Doubt
Profile