A uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
magnetic field inside the cylinder increases linearly from zero at the centre
magnetic field will be maximum at a point on its axis
magnetic field will be maximum at a point on its surface
magnetic field is minimum at a point on its surface
The correct Answer is:a, c
Magnetic field intensity due to this system at a point at a distance from its centre is given as follows:
x<R:B=μ0Ix2πR2
x>R:B=μ0i2πx
Hence magnetic field is zero at x = 0 and option (a) is correct.
Magnetic field is increasing linearly from the centre up to the surface and then further, it decreases inversely proportional to the distance, hence it attains a maximum field at the surface. Thus, option (c) is also correct.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (ASSERTION TYPE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
79 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A long wire in the shape of a cylindrical shell of inner and outer radii R2 and R respectively carries a steady current I in a direction parallel to its length. This current is uniformly distributed across the area of cross-section of the wire. The magnetic field intensity at a point at a distance 3R4 from the axis of the wire is m(μ0IπR).. The value of m is _________.
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View Solution
Knowledge Check
A long cylindrical wire carries a steady current which is uniformly distributed across its cross section. Which of the following is true?
AMagnetic field is zero at the centre.BElectric field is zero at the centre.CElectric field just outside the cylinder is zero.DMagnetic field just outside the cylinder is zero.A cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
Aμ0I2π(R−x)Bμ0I2πxCμ0I2π(R+x)Dnone of theseA long straight wire of radius R carries a steady current which is uniformly distributed through the cross-section of the wire. The magnitudes of the magnetic field at distance r1 and r2 from the centre of the wire are B1 and B2 respectively. Then
AB1B2=r1r2,ifr1<R and r2<RBB1B2=r1r2,ifr1>R and r2>RCB1B2=r2r1,ifr1<R and r2<RDnone of these
A long straight conducting solid cylindrical wire of radius R carries a steady current / that is uniformly distributed throughout the cross section of the wire. Choose the correct graph of magnetic field B versus r (where r is distance from the axis of the wire)
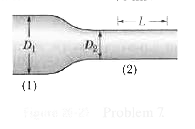
View SolutionFigure 26-21 shows wire section 1 of diameter D1=4.00R and wire section 2 of diameter D2=1.75R, connected by a tapered section. The wire is Copper and carries a current. Assume that the current is uniformly distributed across any cross-sectional area through the wire's width. The electric potential change V along the length L= 2.00 m shown in section 2 is 10.0μV. The number of charge carners per unit volume is 8.49×1028m−3. What is the drift speed of the conduction electrons in section 1?
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
View Solution
