Two inclined frictionless tracks, one gradual and the other steep meet at O, from where two stones are allowed to slide down from rest, one on each track. Will the stones reach the bottom at the same time ? Will they reach there with the same speed ? Explain.
To solve the problem of whether two stones sliding down frictionless inclined tracks will reach the bottom at the same time and with the same speed, we can follow these steps:
Step 1: Understand the Setup
We have two inclined tracks meeting at point O. One track is gradual (let's call it Track 1) and the other is steep (Track 2). Both stones start from rest at point O.
Step 2: Analyze Forces Acting on the Stones
Since both tracks are frictionless, the only force acting on the stones is gravity. The gravitational force can be resolved into two components: one perpendicular to the incline (normal force) and one parallel to the incline (which causes the acceleration down the track).
Step 3: Determine the Acceleration of Each Stone
For each stone, the acceleration along the incline can be calculated using the formula:
- For Track 1 (gradual): a1=gsin(θ1)
- For Track 2 (steep): a2=gsin(θ2)
Where g is the acceleration due to gravity and θ1 and θ2 are the angles of inclination for Track 1 and Track 2, respectively.
Step 4: Use Conservation of Energy to Find Final Speeds
Using the principle of conservation of mechanical energy, we can find the final speeds of both stones when they reach the bottom of their respective tracks.
For both tracks, the change in potential energy equals the change in kinetic energy:
- For Track 1:
12mv21=mgh⟹v1=√2gh
- For Track 2:
12mv22=mgh⟹v2=√2gh
Since both stones start from the same height h, they will both have the same final speed:
v1=v2=√2gh
Step 5: Calculate the Time Taken to Reach the Bottom
Using the kinematic equation v=u+at (where u=0 since they start from rest), we can express the time taken for each stone to reach the bottom:
- For Track 1:
t1=v1a1=√2ghgsin(θ1)
- For Track 2:
t2=v2a2=√2ghgsin(θ2)
Step 6: Compare the Times
To compare the times:
t1t2=√2ghgsin(θ1)÷√2ghgsin(θ2)=sin(θ2)sin(θ1)
Since θ1 and θ2 are different, t1 and t2 will not be equal. Therefore, the stones will not reach the bottom at the same time.
Conclusion
- Final Speed: Both stones will reach the bottom with the same speed √2gh.
- Time Taken: The stones will not reach the bottom at the same time; the time taken depends on the angles of inclination.
We have two inclined tracks meeting at point O. One track is gradual (let's call it Track 1) and the other is steep (Track 2). Both stones start from rest at point O.
Since both tracks are frictionless, the only force acting on the stones is gravity. The gravitational force can be resolved into two components: one perpendicular to the incline (normal force) and one parallel to the incline (which causes the acceleration down the track).
For each stone, the acceleration along the incline can be calculated using the formula:
- For Track 1 (gradual): a1=gsin(θ1)
- For Track 2 (steep): a2=gsin(θ2)
Using the principle of conservation of mechanical energy, we can find the final speeds of both stones when they reach the bottom of their respective tracks.
- For Track 1:
12mv21=mgh⟹v1=√2gh
- For Track 2:
12mv22=mgh⟹v2=√2gh
v1=v2=√2gh
Using the kinematic equation v=u+at (where u=0 since they start from rest), we can express the time taken for each stone to reach the bottom:
- For Track 1:
t1=v1a1=√2ghgsin(θ1)
t2=v2a2=√2ghgsin(θ2)
To compare the times:
t1t2=√2ghgsin(θ1)÷√2ghgsin(θ2)=sin(θ2)sin(θ1)
- Final Speed: Both stones will reach the bottom with the same speed √2gh.
- Time Taken: The stones will not reach the bottom at the same time; the time taken depends on the angles of inclination.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Additional Exercises
3 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - higher order thinking skills
10 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Advanced Problems For Competitions
20 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Two inclined frictionless tracks, one gradual and the other steep meet at A from where to stones are allowed to slide down from rest, one on each track (fig.) Will hte stones reach the bottom at the same time? Will they reach there with the same speed? Explain, given θ1=30∘, θ92)=60∘ and h=10m. What are the speeds and time taken by the two stones?
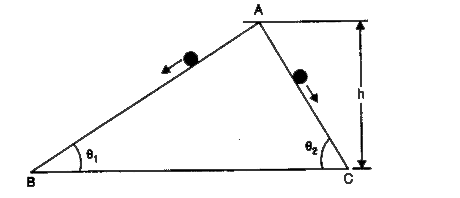
View SolutionTwo inclined frictionless tracks , one gradual and the other sleep meet at A from where two stones are allowed to slide down from rest. One on each track as shown in figure. Which of the following statement is correct?

View Solution
Knowledge Check
Two inclined frictionless tracks, one gradual and the other steep meet at a from where two stones are allowed to slide down from rest, one on each track as shown in Figure. Which of the following statement is correct ?
 .ABoth the stone reach the botton at the same time but not with the same speed.BBoth the stone reach the bottom with the same speed and stone I reaches the bottom earlier than stone II Figure.CBoth the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.DBoth the stones reach the bottom at different times and with different speeds.
.ABoth the stone reach the botton at the same time but not with the same speed.BBoth the stone reach the bottom with the same speed and stone I reaches the bottom earlier than stone II Figure.CBoth the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.DBoth the stones reach the bottom at different times and with different speeds.Two inclined frictionless tracks, one gradual and other steep meet at 'A' from where two stones are allowed to slide down from rest, one on each track as shown in figure. The speed of two stones on reaching at bottom are v1andv2 respectively. v1&v2 are related as
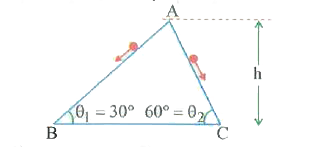 Av1>v2Bv1<v2Cv1=v2Ddata insufficient
Av1>v2Bv1<v2Cv1=v2Ddata insufficientAn object is placed on the surface of a smooth inclined plane of inclination . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination , it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction is given by -
Aμ=tanθ[1−1n2]Bμ=cotθ[1−1n2]Cμ=tanθ[1−1n2]1/2Dμ=cotθ[1−1n2]1/2
A stone is projected horizontally from the top of a towar. At the same time , another stone is dropped down from the same height . Which ball will reach the ground earlier? Will they hit the ground with same velocity ?
View SolutionA and B are two identical rings released from the top of an inclined plane . A slides down and B rolls down. Then which reaches the bottom first ?
View SolutionTwo spherical bobs, one metallic and the other of glass, of the same size are allowed to fall freely from the same height above the ground. Which of the two would reach earlier and why?
View SolutionA smooth inclined plane is inclined at an angle θ with the horizontal. A body starts from rest and slides down the inclined surface. The time taken by the body to reach the bottom is
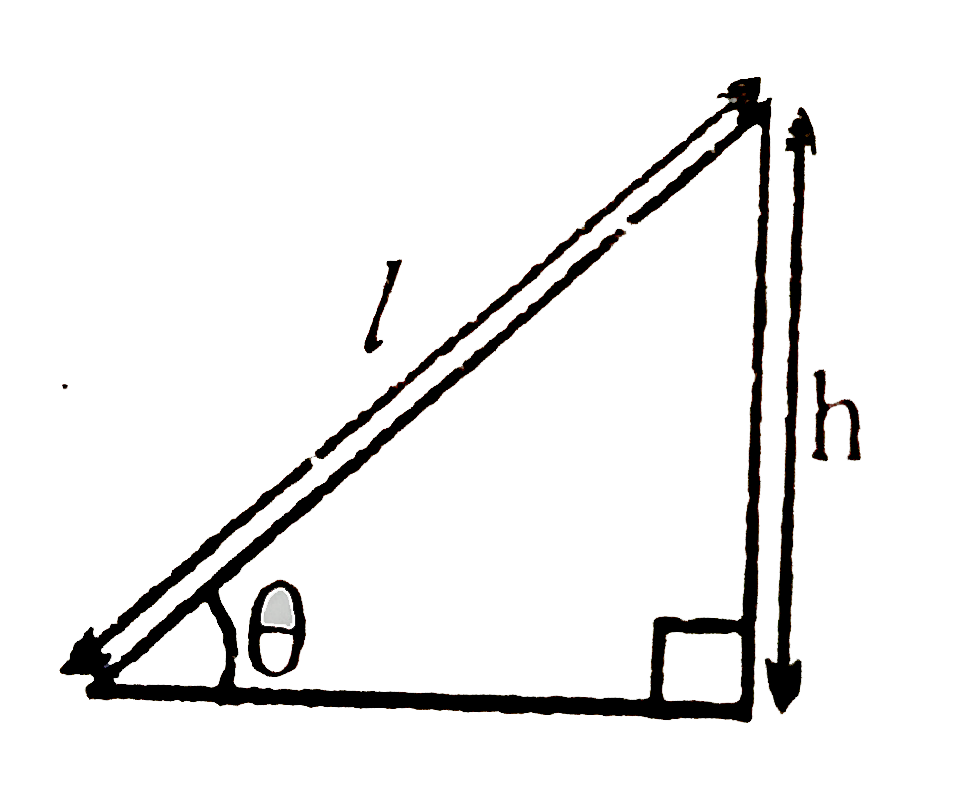
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ. It takes time t to reach the bottom. If the same object is allowed to slide down a rough inclined plane of inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by:-
View Solution
