Two inductors L1(inductors 1 mH, internal resistance 3 Ω) and L2 (inductance 2mH, internal resistance 4Ω),and a resistor R(resistance12ω) are all connected in parallelacross a 5 V battery. The circuit is switched on at time t=0. The ratio of the maximum to the minimum current (Imax/Imin) drawn from the battery is
To solve the problem, we need to find the ratio of the maximum to the minimum current drawn from the battery when two inductors and a resistor are connected in parallel.
1. Identify the Components and Their Values:
- Inductor L1: Inductance =1mH, Internal Resistance r1=3Ω
- Inductor L2: Inductance =2mH, Internal Resistance r2=4Ω
- Resistor R=12Ω
- Voltage of the battery V=5V
2. Calculate the Total Resistance in Parallel:
The total resistance Req for resistors in parallel is given by:
1Req=1R+1r1+1r2
Substituting the values:
1Req=112+13+14
Finding a common denominator (which is 12):
1Req=112+412+312=812
Thus,
Req=128=1.5Ω
3. Calculate the Maximum Current Imax:
The maximum current occurs when the inductors are fully energized (steady state). Using Ohm's law:
Imax=VReq=5V1.5Ω=103A
4. Calculate the Minimum Current Imin:
The minimum current occurs when the inductors behave like open circuits (at the moment of switching on). The only current flowing is through the resistors:
Imin=VR=5V12Ω=512A
5. Calculate the Ratio of Maximum to Minimum Current:
ImaxImin=103512=103×125=10×123×5=12015=8
Final Answer:
The ratio of the maximum to the minimum current drawn from the battery is 8.
- Inductor L1: Inductance =1mH, Internal Resistance r1=3Ω
- Inductor L2: Inductance =2mH, Internal Resistance r2=4Ω
- Resistor R=12Ω
- Voltage of the battery V=5V
The total resistance Req for resistors in parallel is given by:
1Req=1R+1r1+1r2
Substituting the values:
1Req=112+13+14
Finding a common denominator (which is 12):
1Req=112+412+312=812
Thus,
Req=128=1.5Ω
The maximum current occurs when the inductors are fully energized (steady state). Using Ohm's law:
Imax=VReq=5V1.5Ω=103A
The minimum current occurs when the inductors behave like open circuits (at the moment of switching on). The only current flowing is through the resistors:
Imin=VR=5V12Ω=512A
ImaxImin=103512=103×125=10×123×5=12015=8
The ratio of the maximum to the minimum current drawn from the battery is 8.
Topper's Solved these Questions
Similar Questions
Two inductors L1 (inductance 1 mH, internal resistance 3Ω)and L2 (inductance 2 mH, internal resistance 4Ω), and a resistance R (resistance 12Ω)are all connected in parallel across a 5V battery . The circuit is switched on at time t=0. The ratio of the maximum to the minimum current (Imax/Imin) drawn from the battery is :
View SolutionA 5 V battery with internal resistance 2Ω and a 2V battery with internal resistance 1Ω are connected to a 10Ω as shown in the figure.
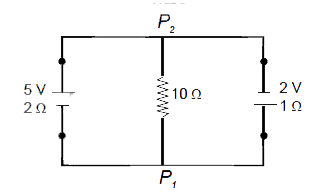
The current in the 10Ω resistance isView Solution
Knowledge Check
- Question 1 - Select One
A 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.

The current in the 10Ω resistor isA0.27AP2→P1B0.03AP1→P2C0.03AP2→P1D0.27AP1→P2 - Question 2 - Select One
A 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.

The current in the 10Ω resistor isA0.27 AB0.05 AC0.25 AD0.3 A - Question 3 - Select One
Two batteries, one of emf 18 V and internal resistance 2 Ω and the other of emf 12 V and internal resistance 1Ω , are connected in parallel as shown in Fig. The voltmeter V will record a reading of
 A15VB14VC30VD18V
A15VB14VC30VD18V
7 V battery with internal resistance 2Ωand3V battery with internal resistance 1Ω are connected to a 10Ω resistors as shown in figure, the current in 10Ω resistor is
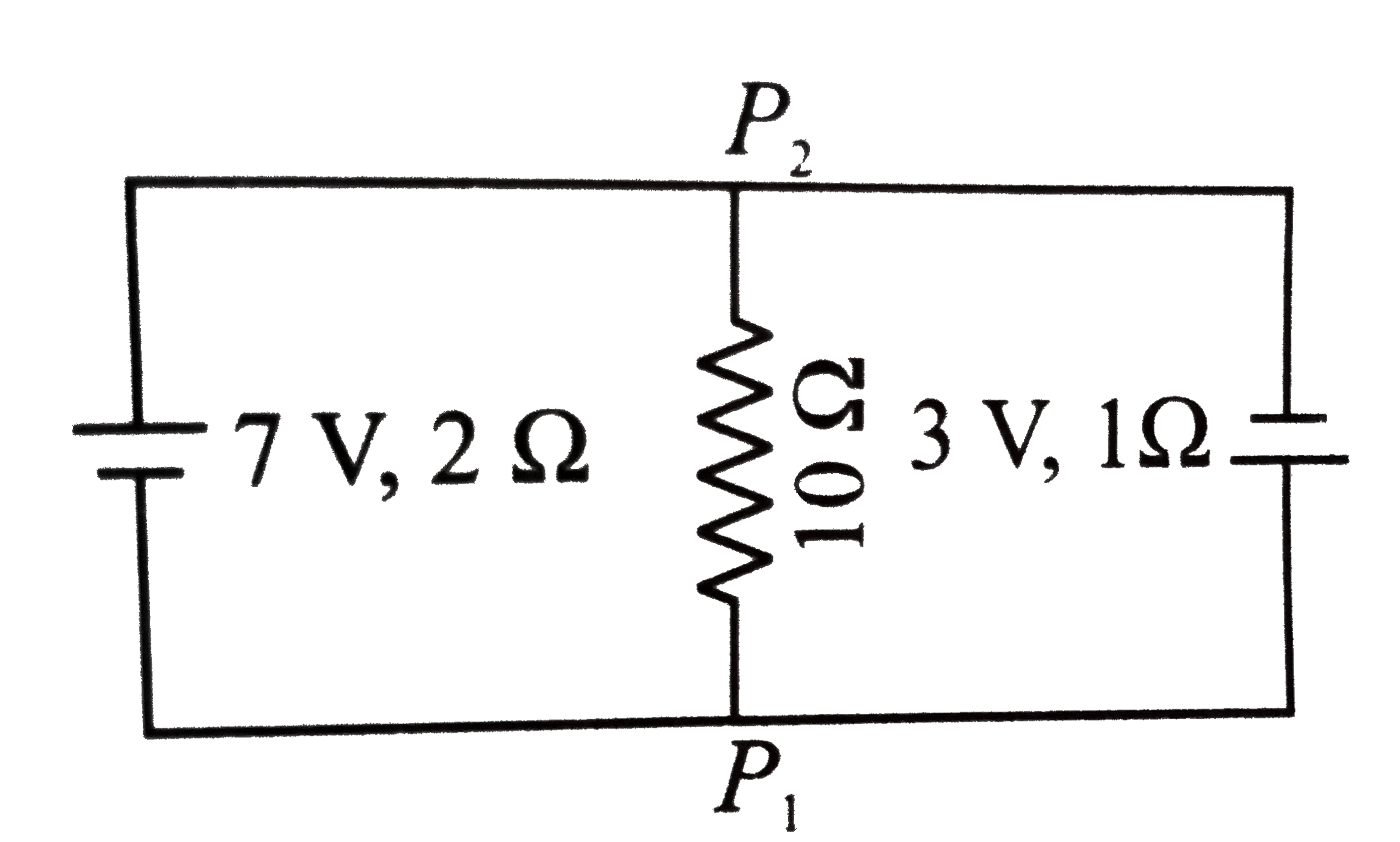 View Solution
View SolutionA coil of inductance 8.4 mH and resistance 6(Ω) is connected to a 12 V battery. The current in the coil is 1.0 A at approximately the time
View SolutionA coil of inductance 8.4mH and resistance 6 Ω is connected to a 12V battery. The current in the coil is 1.0A at approximately the time.
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing thrpough the battery ?
View SolutionA coil of inductance 8.4 mH and resistance 6ω is connected to 12 V battery. The current in the coil is 1 A at approximately the time
View Solution

