Two light strings of length 4 cm and 3 cm are tied to a bob of weight 500 gm. The free ends of the strings are tied to pegs in the same horizontal line and separated by 5 cm. The ratio of tension in the longer string to that in the shorter string is
4:3
3:4
4:5
5:4
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the bob and apply the concept of equilibrium. Here’s a step-by-step solution:
Step 1: Draw the Diagram
First, we need to visualize the situation. Draw a horizontal line representing the distance between the two pegs, which is 5 cm apart. At each end of this line, draw two strings: one of length 4 cm and the other of length 3 cm, both attached to a bob (weight = 500 gm) hanging downwards.
Step 2: Identify the Tensions
Label the tension in the longer string (4 cm) as T1 and the tension in the shorter string (3 cm) as T2.
Step 3: Resolve the Tensions into Components
Since the bob is in equilibrium, we can resolve the tensions into horizontal and vertical components. For the longer string:
- The horizontal component is T1cos(θ)
- The vertical component is T1sin(θ)
For the shorter string:
- The horizontal component is T2cos(90∘−θ)=T2sin(θ)
- The vertical component is T2cos(θ)
Step 4: Apply Equilibrium Conditions
Since the bob is in equilibrium, the horizontal components of the tensions must balance each other:
T1cos(θ)=T2sin(θ)
Step 5: Find the Ratio of Tensions
From the equilibrium condition, we can express the ratio of the tensions:
T2T1=cos(θ)sin(θ)=cot(θ)
Step 6: Determine the Angles
Using the lengths of the strings and the horizontal distance between the pegs, we can find cot(θ):
- The vertical distance from the bob to the peg of the shorter string is 3 cm.
- The vertical distance from the bob to the peg of the longer string is 4 cm.
- The horizontal distance between the two pegs is 5 cm.
Using the right triangle formed by the shorter string:
cot(θ)=adjacentopposite=3 cm4 cm
Step 7: Final Calculation
Thus, we have:
T2T1=cot(θ)=34
Step 8: Ratio of Tensions
To find the ratio of tension in the longer string to that in the shorter string:
T1T2=43
Conclusion
The ratio of tension in the longer string to that in the shorter string is 43.
First, we need to visualize the situation. Draw a horizontal line representing the distance between the two pegs, which is 5 cm apart. At each end of this line, draw two strings: one of length 4 cm and the other of length 3 cm, both attached to a bob (weight = 500 gm) hanging downwards.
Label the tension in the longer string (4 cm) as T1 and the tension in the shorter string (3 cm) as T2.
Since the bob is in equilibrium, we can resolve the tensions into horizontal and vertical components. For the longer string:
- The horizontal component is T1cos(θ)
- The vertical component is T1sin(θ)
- The horizontal component is T2cos(90∘−θ)=T2sin(θ)
- The vertical component is T2cos(θ)
Since the bob is in equilibrium, the horizontal components of the tensions must balance each other:
T1cos(θ)=T2sin(θ)
From the equilibrium condition, we can express the ratio of the tensions:
T2T1=cos(θ)sin(θ)=cot(θ)
Using the lengths of the strings and the horizontal distance between the pegs, we can find cot(θ):
- The vertical distance from the bob to the peg of the shorter string is 3 cm.
- The vertical distance from the bob to the peg of the longer string is 4 cm.
- The horizontal distance between the two pegs is 5 cm.
cot(θ)=adjacentopposite=3 cm4 cm
Thus, we have:
T2T1=cot(θ)=34
To find the ratio of tension in the longer string to that in the shorter string:
T1T2=43
The ratio of tension in the longer string to that in the shorter string is 43.
Similar Questions
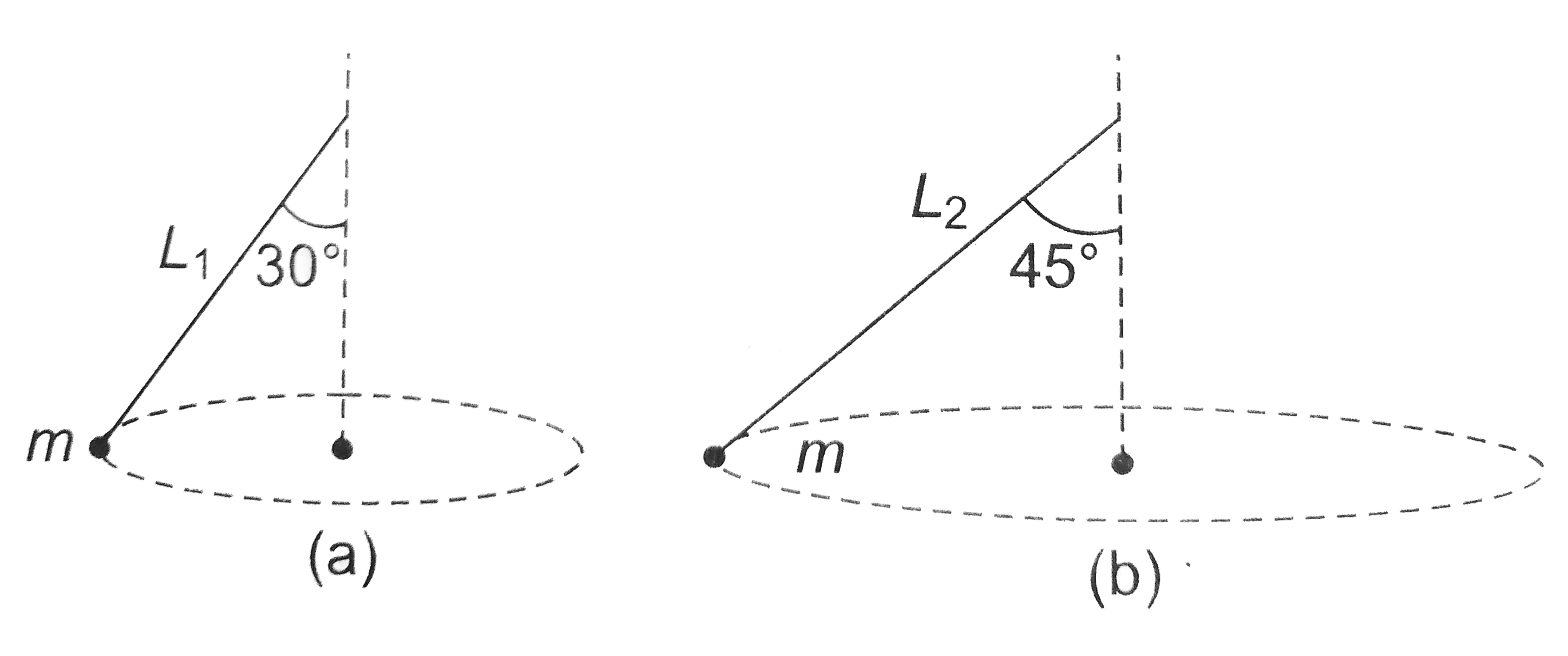
Two partical tied to different strings are whirled in a horizontal circle as shown in figure. The ratio of lengths of the string so that they complete their circular path with equal time period is:
View SolutionA stone of mass 0.1 kg tied to one end of a string lm long is revolved in a horizontal circle at the rate of 10π rev/s. Calculate the tension in the string.
View SolutionA body of mass 50 kg, suspended by two strings of lengths 30 cm and 40 cm fastend to two points in the same horizontal line 50 cm apart, is in equilibrium. Find the tension (in Newtons) in each string.
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA 2 kg stone tied at the end of a string of l m len"gt"h, is whirled along a vertical circle at a constant speed of 4ms−1. The tension in the string has a value of 52 N when the stone is
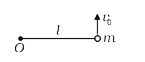
View SolutionA bob in tied to a string of length l & and kept on a horizontal rough surface as shown in the figure when point O of the string is fixed. The bob is given a tangential velocity V0 keeping the string taut as shown in figure. Find the tension in the string as a function of time. The coefficient of kinetic friction is μ.
View SolutionEach of the two strings of length 51.6cm and 49.1cm are tensioned separately by 20N force. Mass per unit length of both the strings is same and equal to 1g/m. When both the strings vibrate simultaneously, the number of beats is
View Solution
A rod is supported horizontally by means of two strings of equal length as shown in figure. If one of the string is cut. Then tension in other string at the same instant will.
View Solution
