Two magnets of different masses and geometry are tied together length wise. When this system is made to oscillate in a uniform magnetic field then time period of oscillation is found to be 4s. Now one of the magnets is reversed and then again tied together length wise. Time period of oscillation in same magnetic field is found to be 3s. Calculate ratio of magnetic moments of magnets.
To solve the problem, we need to analyze the time periods of oscillation of the two magnets when they are combined in different configurations. Let's denote the magnetic moments of the two magnets as M1 and M2.
1. Understanding the Time Period of Oscillation:
The time period T of oscillation of a magnetic dipole in a magnetic field is given by the formula:
T=2π√ImB
where I is the moment of inertia, m is the magnetic moment, and B is the magnetic field strength.
2. Setting Up the Equations:
- For the first configuration (when the magnets are aligned with the same polarity), the time period is given as T1=4s:
T1=2π√I(M1+M2)B(1)
- For the second configuration (when one magnet is reversed), the time period is given as T2=3s:
T2=2π√I(M1−M2)B(2)
3. Squaring Both Equations:
- From equation (1):
T21=4π2I(M1+M2)B
Substituting T1=4:
16=4π2I(M1+M2)B(3)
- From equation (2):
T22=4π2I(M1−M2)B
Substituting T2=3:
9=4π2I(M1−M2)B(4)
4. Rearranging Equations (3) and (4):
- From equation (3):
(M1+M2)=4π2I16B=π2I4B(5)
- From equation (4):
(M1−M2)=4π2I9B(6)
5. Dividing Equations (5) and (6):
Now, we can divide equation (5) by equation (6):
M1+M2M1−M2=π2I4B4π2I9B=916
6. Cross-Multiplying:
9(M1−M2)=16(M1+M2)
Expanding this gives:
9M1−9M2=16M1+16M2
Rearranging terms:
9M1−16M1=16M2+9M2
−7M1=25M2
Thus, we find:
M1M2=257
Final Result:
The ratio of the magnetic moments of the two magnets is:
M1M2=257
The time period T of oscillation of a magnetic dipole in a magnetic field is given by the formula:
T=2π√ImB
where I is the moment of inertia, m is the magnetic moment, and B is the magnetic field strength.
- For the first configuration (when the magnets are aligned with the same polarity), the time period is given as T1=4s:
T1=2π√I(M1+M2)B(1)
- For the second configuration (when one magnet is reversed), the time period is given as T2=3s:
T2=2π√I(M1−M2)B(2)
- From equation (1):
T21=4π2I(M1+M2)B
Substituting T1=4:
16=4π2I(M1+M2)B(3)
- From equation (2):
T22=4π2I(M1−M2)B
Substituting T2=3:
9=4π2I(M1−M2)B(4)
- From equation (3):
(M1+M2)=4π2I16B=π2I4B(5)
- From equation (4):
(M1−M2)=4π2I9B(6)
Now, we can divide equation (5) by equation (6):
M1+M2M1−M2=π2I4B4π2I9B=916
9(M1−M2)=16(M1+M2)
Expanding this gives:
9M1−9M2=16M1+16M2
Rearranging terms:
9M1−16M1=16M2+9M2
−7M1=25M2
Thus, we find:
M1M2=257
The ratio of the magnetic moments of the two magnets is:
M1M2=257
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - REVISION EXERCISE (VERY SHORT ANSWER QUESTION)
65 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - REVISION EXERCISE (ADDITIONAL QUESTION)
5 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - NCERT FILE (ADDITIONAL EXERCISE)
18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Chapter Practice Test
9 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST
13 Videos
Similar Questions
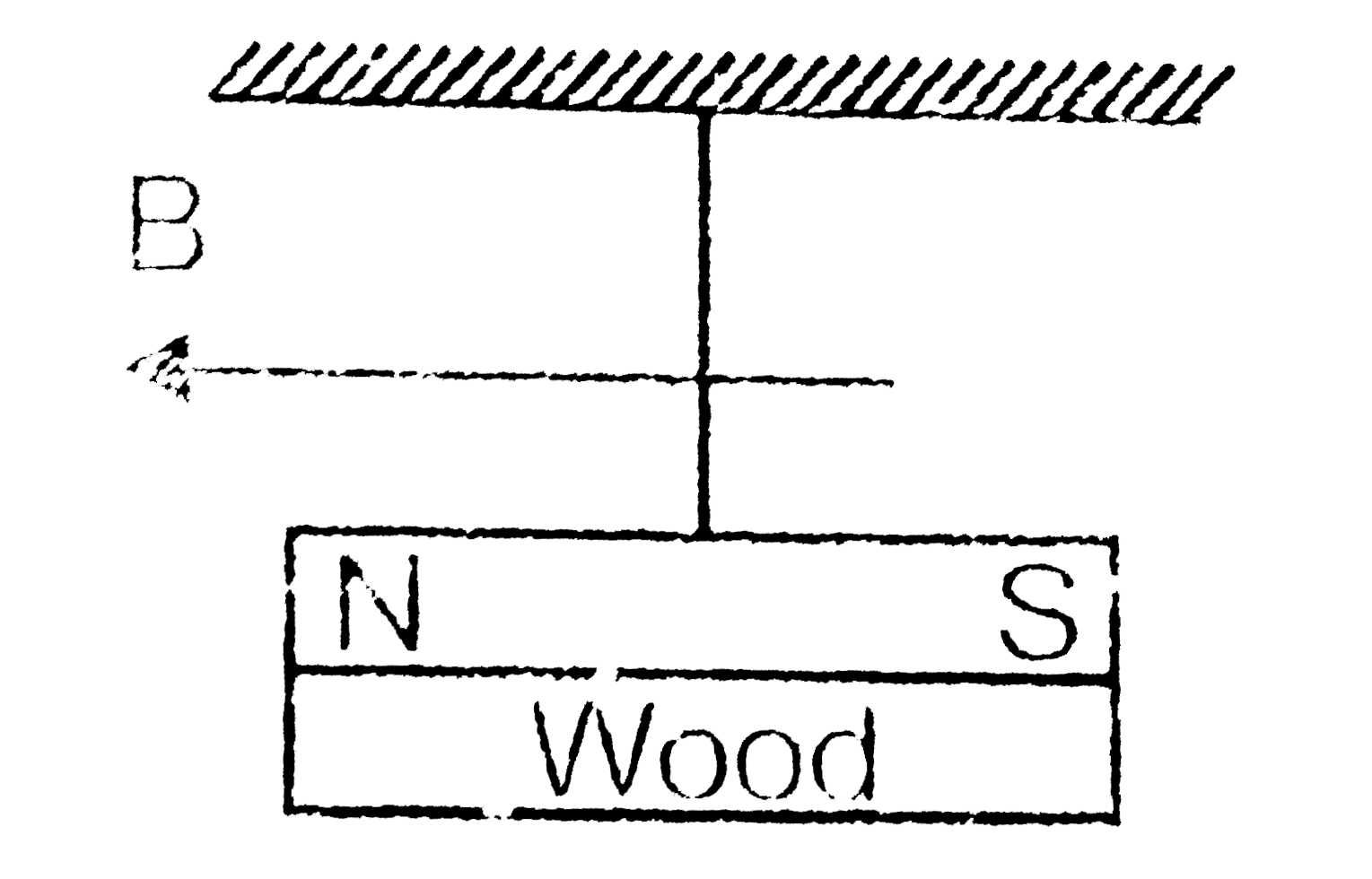
A bar magnet oscillates in a region of uniform magnetic field with time period T . Now , a piece of wood identical in all respects in terms of mass and length is joined with bar magnet as shown . The new time period of oscillation is
View SolutionA bar magnet suspended freely has period of oscillation of 2s. Now, the bar magnet is broken into equal halves and one-half is suspended to oscillate freely in the same magnetic field. Find the time period of oscillation of this half of the magnet.
View Solution
Knowledge Check
Time period of oscillation of a magnetic needle is
AT=√TMBBT=2π√IMBCT=2π√MBIDT=π√MBIThe perio of oscillation of a magnet in vibration magnetometer is 2 sec. The period of oscillation of a magnet whosr magnetic moment is four times that of the first magnet is
A1secB4secC8secD0.5secA thin magnetic iron rod of length 30 cm is suspended in a uniform magnetic field. Its time period of oscillation is 4s. It is broken into three equal parts. The time period in second of oscillation of one part. When suspended in the same magnetic field, is
A1√3B2√3C√3D4√3
Two bar magnets having same geometry with magnetic moments M and 2M, are firstly placed in such a way what their similar poles are same side then its time period of oscillation is T1. Now the polarity of one of the magnet is reversed then time period of oscillation will be:-
View SolutionThe factors on which the period of oscillation of a "bar" magnet in uniform magnetic field depend
View SolutionThe period of oscillations of a magnet is 2 sec. When it is remagnetised so that the pole strength is 4 times its period will be
View SolutionThe magnetic moments of two bar magnets of same size are in the ratio 1:2. When they are placed one over the other with their similar poles together, then their perlod of oscillation in a magnetic field is 3s. If one of the magnets is reversed, then the period of oscillation in the same field will be q
View SolutionTwo bar magnets having same geometry with magnetic moments M and 2M, are firstly placed in such a way what their similar poles are same side then its time period of oscillation is T1. Now the polarity of one of the magnet is reversed then time period of oscillation will be:-
View Solution
