Two masses M and m are attached to a vertical axis by weightless threads of combined length l . They are set in rotational motion in a horizontal plane about this axis with constant angular velocity ω . If the tensions in the threads are the same during motion, the distance of M from the axis is
(M+mm)l
(M+mM)l
(MMm)l
(MM+m)l
The correct Answer is:D
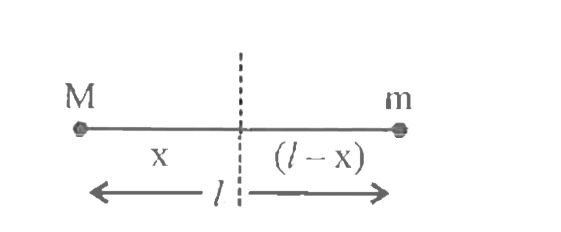
Suppose that M is at a distance x from the axis of rotation, so that the distance of m from the axis
=l−x
They are moving with the same angular velocity ω.
∴ The tensions in the threads will be
T1=Mxω2andT2=m(l−x)ω2 ∴Mx=ml=mx
∴x(M+m)=ml ∴x=mlM+m
Topper's Solved these Questions
Similar Questions
Two balls of mass "M=9g" and "m=3g" are attached by massless threads "AO" and "OB" .The length "AB" is "1m" .They are set in rotational motion in a horizontal plane about a vertical axis at "O" with constant angular velocity ω .The ratio of length "AO" and [OB((AO)/(OB)) for which the tension in threads are same will be 1) 1/3 2) 3 3) 2/3 4) 3/2
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View Solution
Knowledge Check
A particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
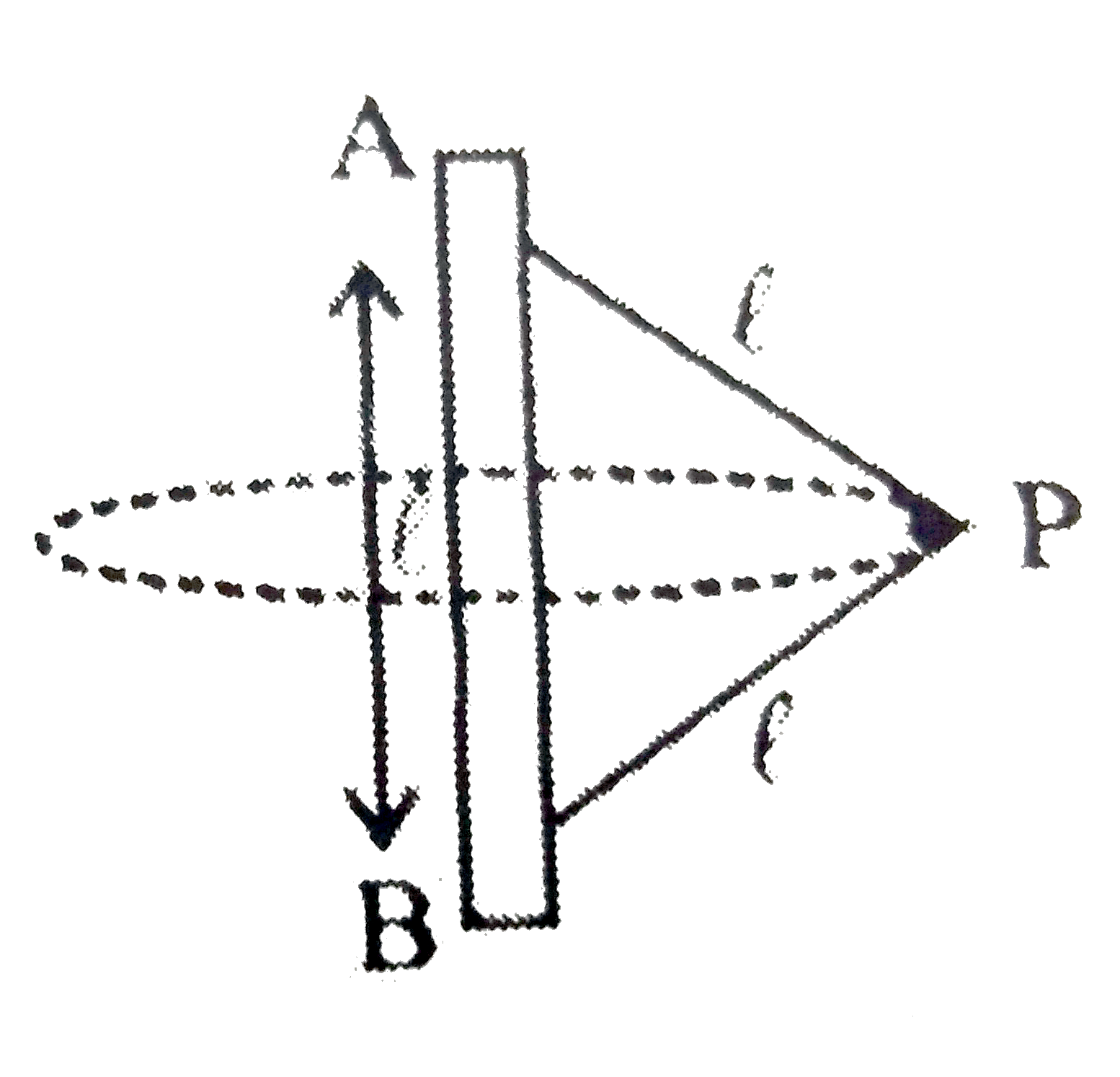 AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remain taut only if ω≥√2gl
AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remain taut only if ω≥√2glA particle P of mass m is attached to a vertical axis by two strings AP and BP of legth l each. The separation AB=l, rotates around the axis with an angular velocity ω. The tension in the two string are T1 and T2. Then
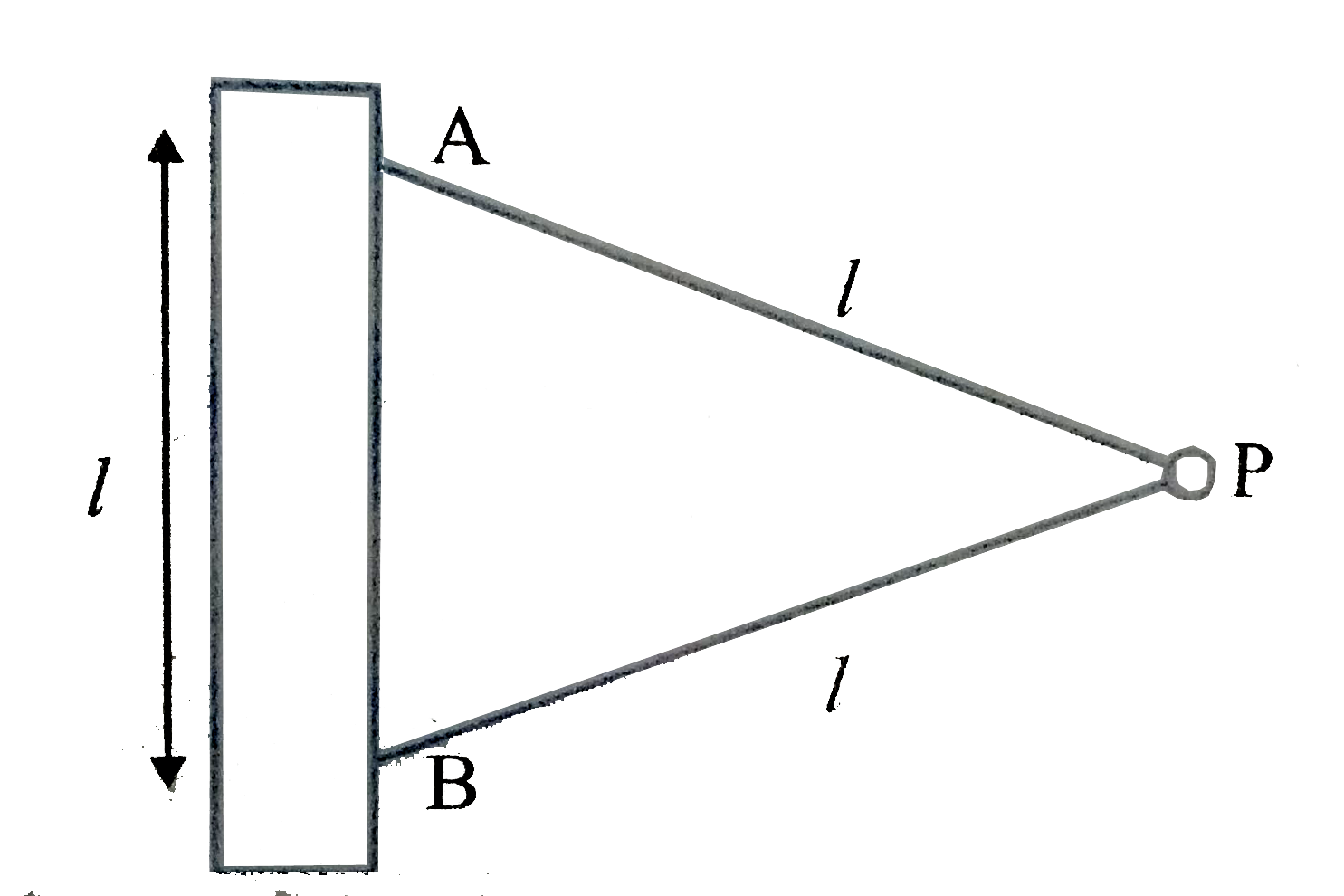 AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remains taut only if ω≥√2g/l
AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remains taut only if ω≥√2g/lA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?

View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform rod AB of length 2l and mass m is rotating in a horizontal plane about a vertical axis through A, with angular velocity ω, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
View SolutionA uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency ω. The tension at its axis is
View Solution
