Two balls of mass "M=9g" and "m=3g" are attached by massless threads "AO" and "OB" .The length "AB" is "1m" .They are set in rotational motion in a horizontal plane about a vertical axis at "O" with constant angular velocity ω .The ratio of length "AO" and [OB((AO)/(OB)) for which the tension in threads are same will be 1) 1/3 2) 3 3) 2/3 4) 3/2
Step by step video & image solution for Two balls of mass "M=9g" and "m=3g" are attached by massless threads "AO" and "OB" .The length "AB" is "1m" .They are set in rotational motion in a horizontal plane about a vertical axis at "O" with constant angular velocity omega .The ratio of length "AO" and [OB((AO)/(OB)) for which the tension in threads are same will be 1) 1/3 2) 3 3) 2/3 4) 3/2 by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?
 View Solution
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View Solution
Knowledge Check
- Question 1 - Select One
Two masses M and m are attached to a vertical axis by weightless threads of combined length l . They are set in rotational motion in a horizontal plane about this axis with constant angular velocity ω . If the tensions in the threads are the same during motion, the distance of M from the axis is
AMlM+mBmlM+mCM+mMlDM+mml - Question 2 - Select One or More
A small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
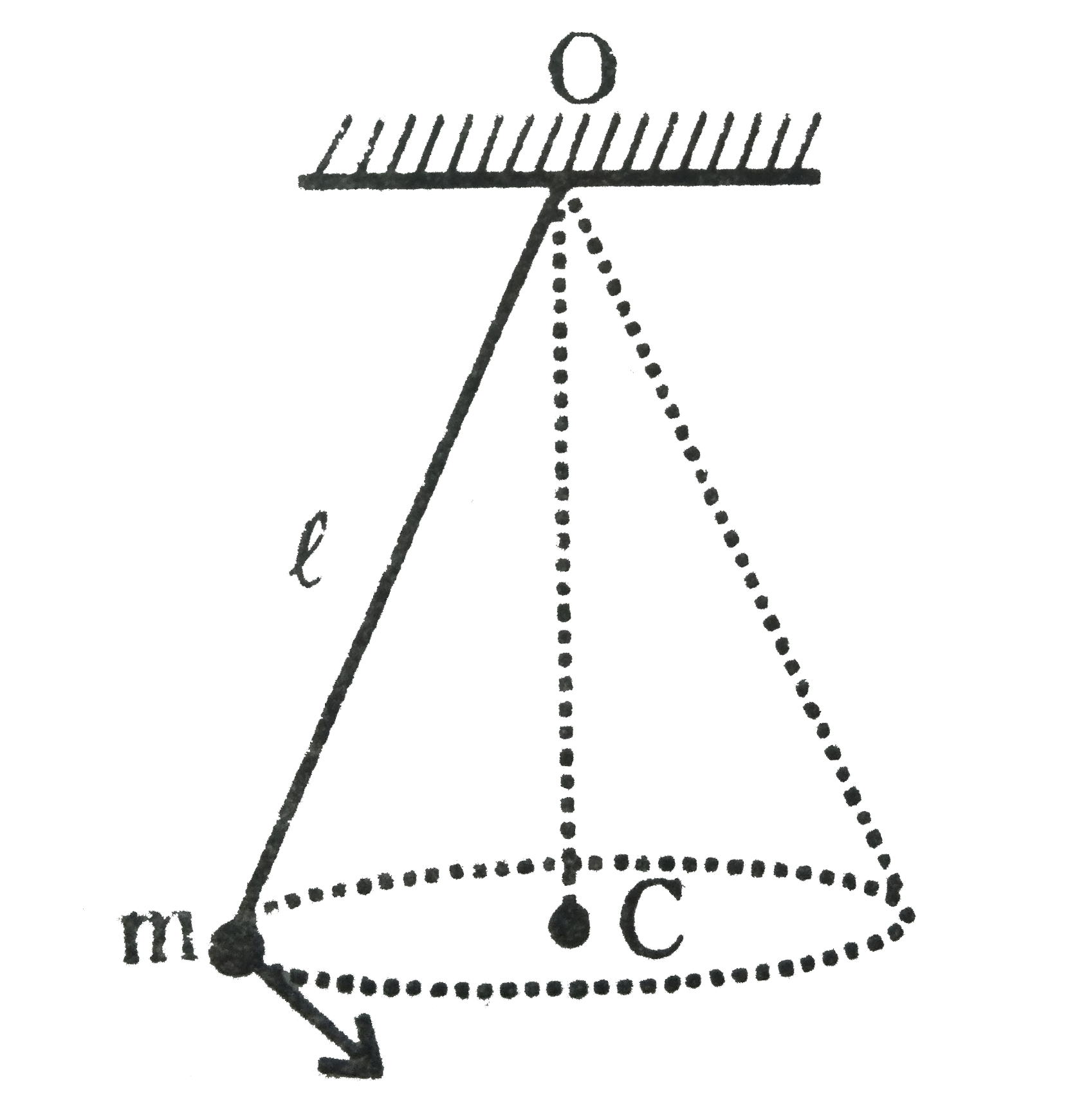 .Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
.Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved - Question 3 - Select One
A thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
Aω(M−2m)M+2mBωMM+2mCω(M+2m)MDωMM+m
A particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
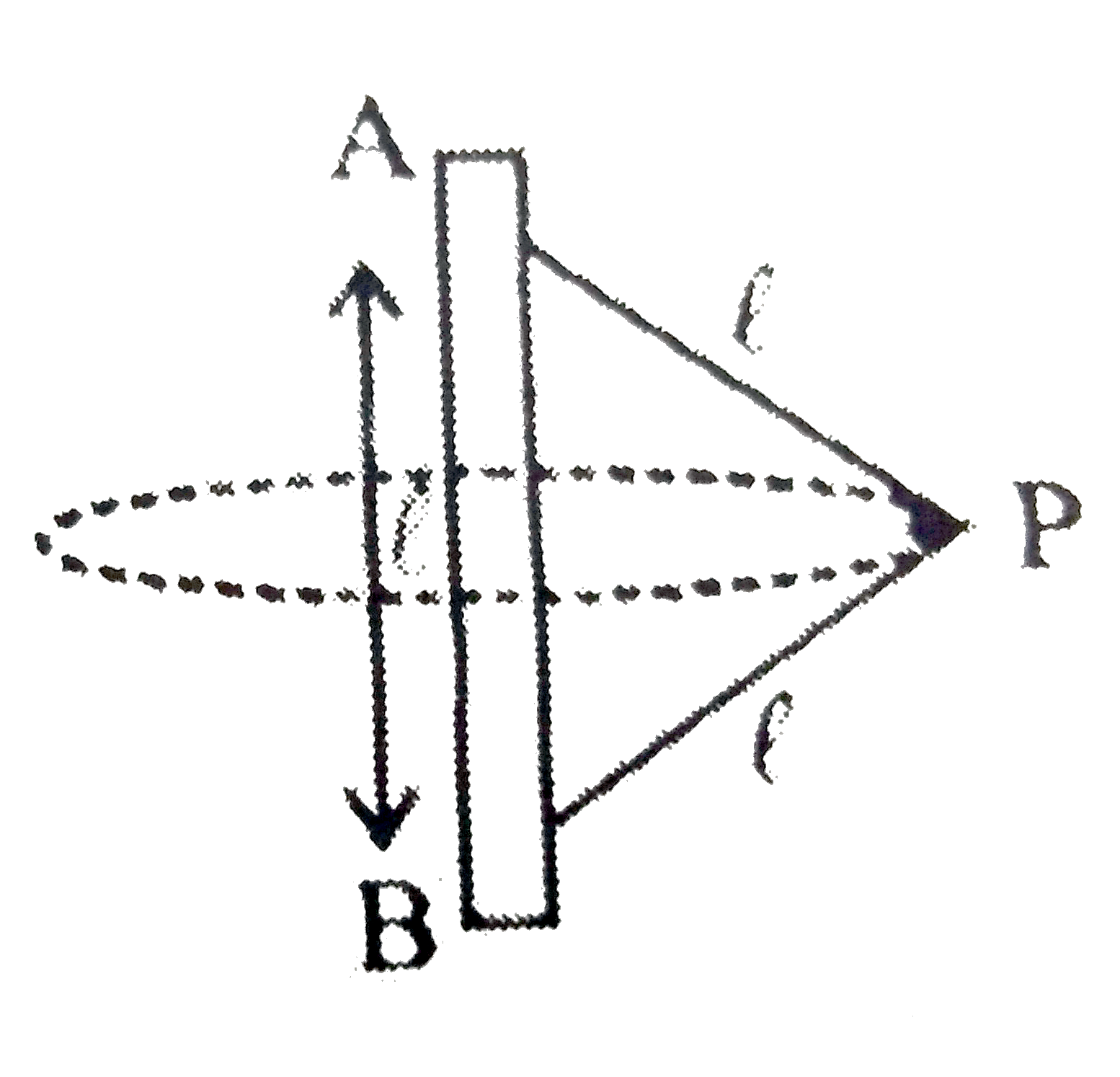 View Solution
View SolutionTwo balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
View SolutionA ball of mass (m) 0.5g is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is
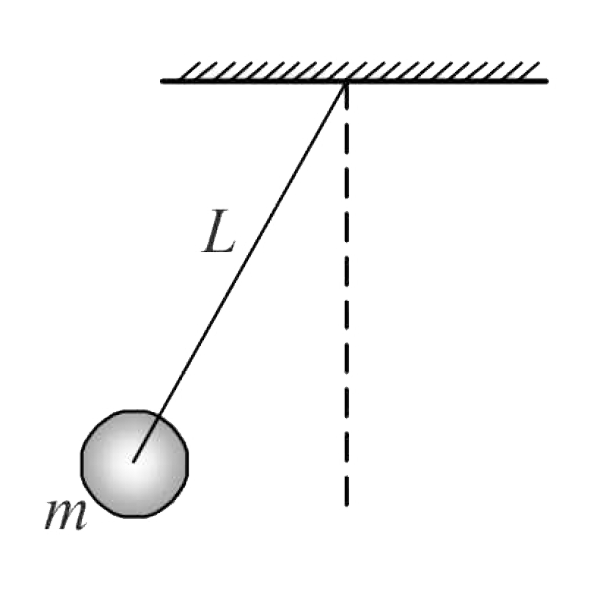 View Solution
View Solution
