Two masses, m1 and m2 , are moving with velocities v1 and v2. Find their total kinetic energy in the reference frame of centre of mass.
K=12m1v21c+12m2v22c………..i
where v1c and v2c are velocities relatives to the CM
v1c=v1−vcm=v1−(m1v1+m2v2m1+m2)=m2(v1−v2)m1+m2
v2c=v2−vCM=v2−(m1v1+m2v2m1+m2)=m1(v2−v1)m1+m2
putting these eqn i K=12m1m2(m1+m2)(v1−v2)2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.223videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.324videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples13videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Two bodies of equal masses are moving with uniform velocities v and 2v. Find the ratio of their kinetic energies
View SolutionTwo masses mA and mB moving with velocities vA and vB in opposite direction collide elastically after that the masses mA and mB move with velocity vB and vA respectively. The ratio (mA/mB) is
View SolutionA bomb at rest explodes into two parts of masses m1 and m2. If the momentums of the two parts be P1 and P2, then their kinetic energies will be in the ratio of:
View SolutionA stationary particle explodes into two particle of a masses m1andm2 which move in opposite direction with velocities v1andv2. The ratio of their kinetic energies E1/E2 is
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionTwo balls with masses m1=3 and m2=5kg have initial velocities v1=v2=5m/s in the directions shown in figure. They collide at the origin.
a. find the velocioty of the CM 3s before the collision.
b. Find the position of the CM 2s after the collision.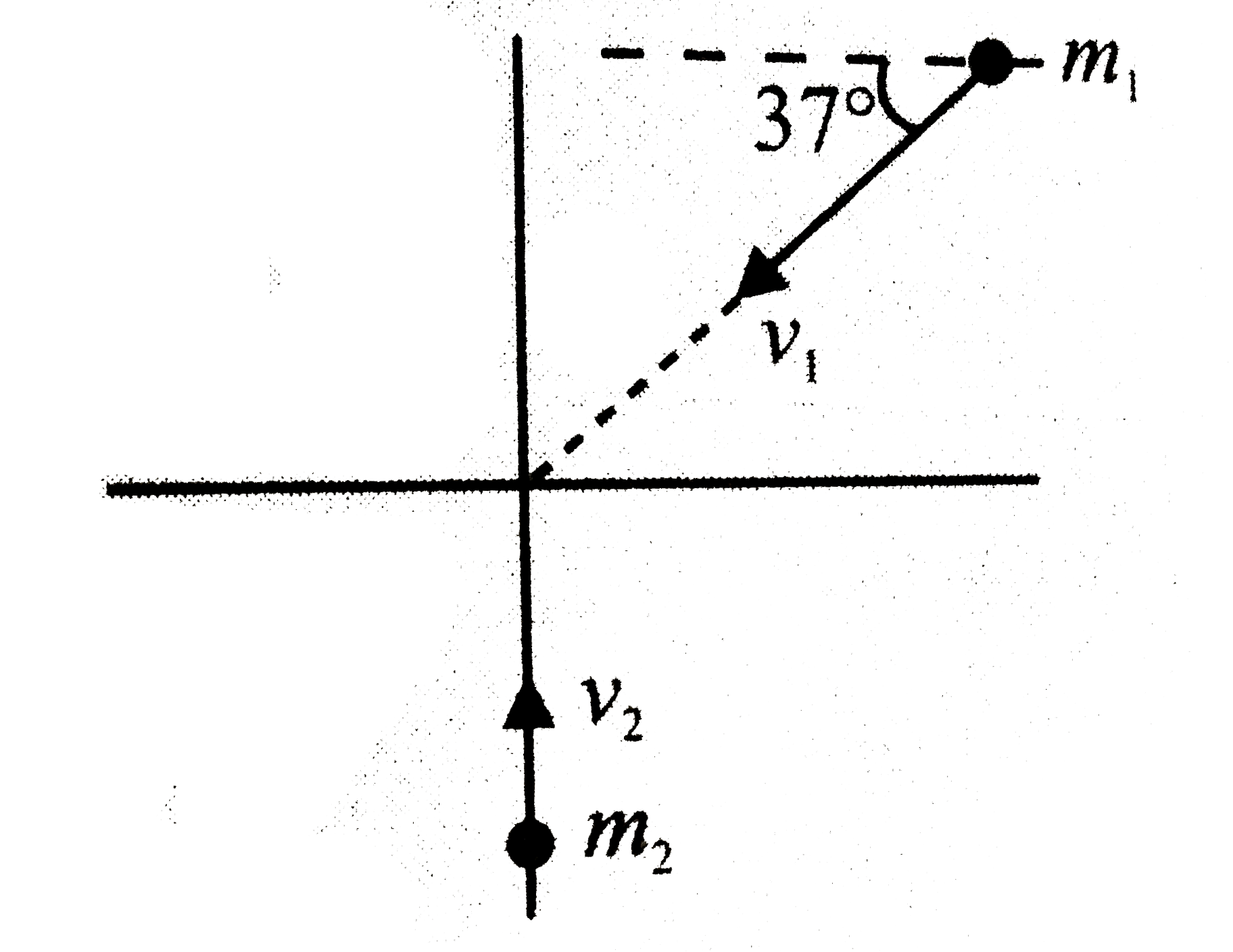 View Solution
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionTwo particles of masses m1,m2 move with initial velocities u1 and u2. On collision, one of the particles get excited to higher level, after absording enegry. If final velocities of particles be v1 and v2 then we must have
View SolutionTwo particles of masses m1,m2 move with initial velocities u1andu2. On collision, one of the particles get excited to higher level, after absorbing energy ε. If final velocities of particles be v1 andv2, then we must have
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their inertia.
View Solution

