Let there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle A starts with a velocity v1 towards line AB, particle B starts with the velocity v2, towards line BC and particle C starts with velocity v3 towards line CA. Find the displacement of the centre of mass of the three particles A,B and C after time t. What would it be if v1=v2=v3?
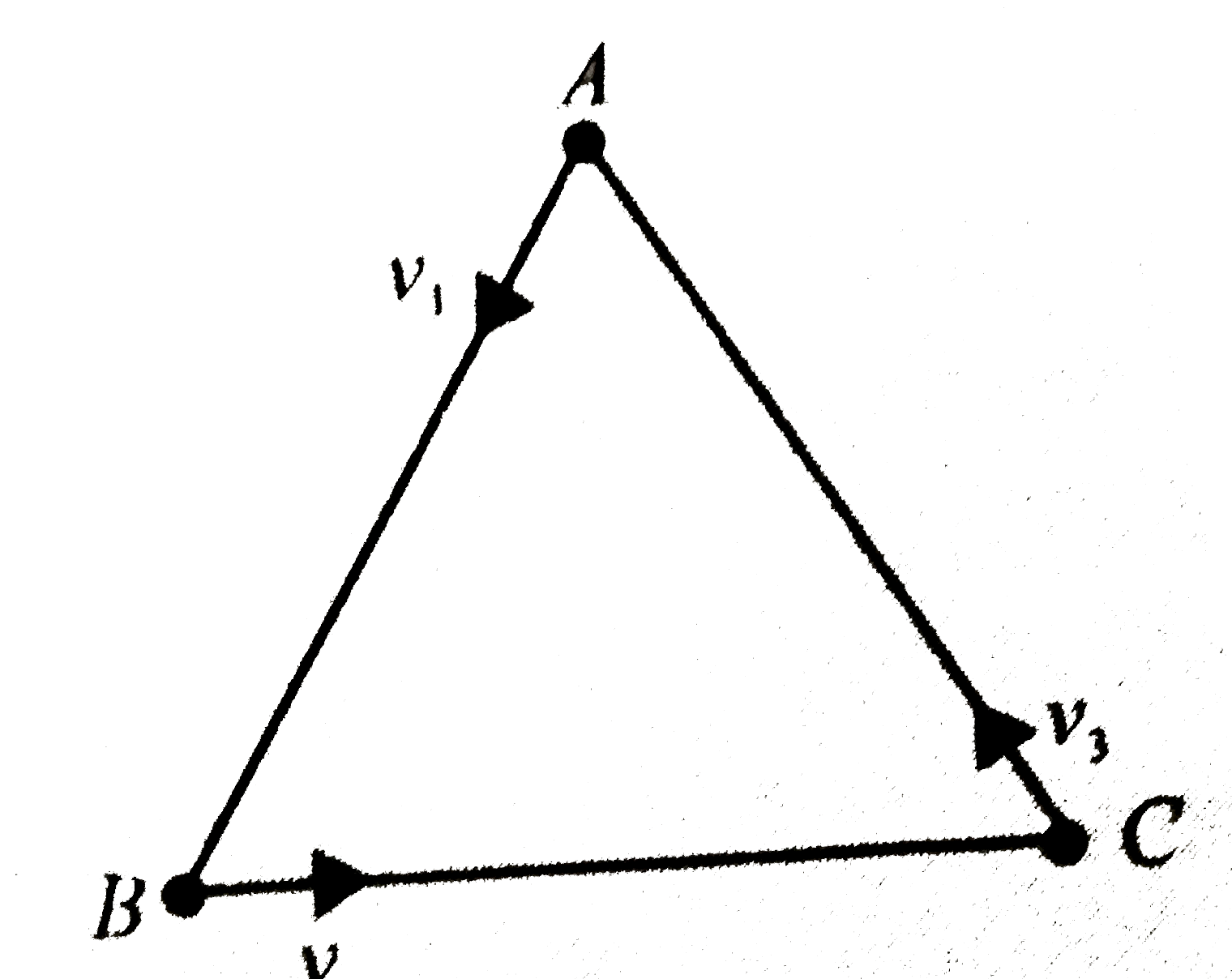
First we write the three velocities in vectorial form, taking right direction as positive x-axis and upwards as positive y-axis.
→–––(1)=−12v1ˆi−√32v1ˆj
→v2=v2ˆi,→v3=12v3ˆi+√32v3ˆj
Thus the velocity of centre of mass of the system is
→vCM=→v1+→v2+→v33
=(v2−12v1−12v3)ˆi+√32(v3−v1)ˆj which can be written as →vCM=vxˆi+vyˆj
Thus displacement of the centre of mass in time t is △→r=vxtˆi+vytˆj
If v1=v2=v3=v we have
→vCM=0
Therefore there is no displacement of centre of mass of the system.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
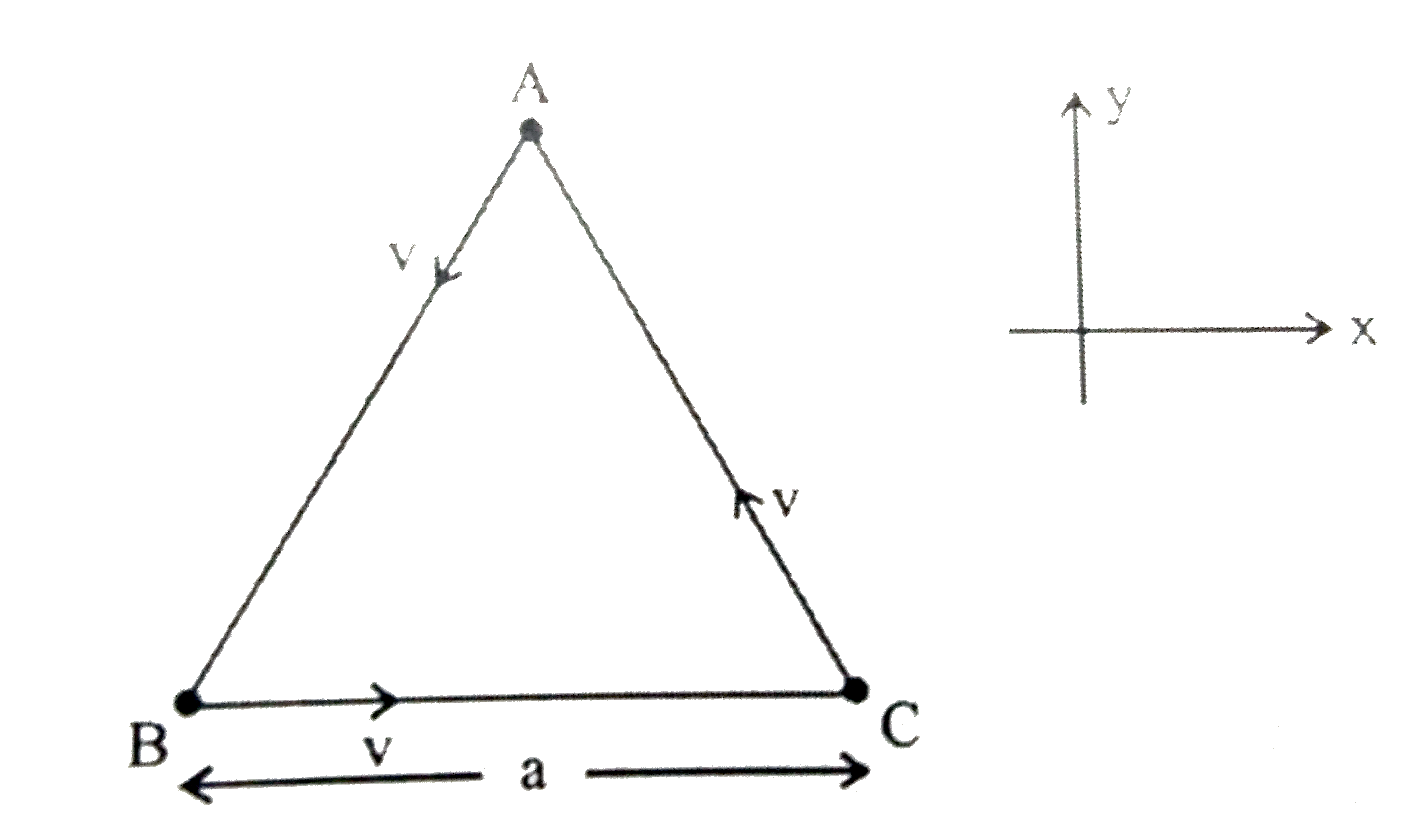
Three particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of
View SolutionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionThre identical masses are kept at the corners of an equilateral triangle ABC. A moves towards B with a velocity V, B moves towards C with velocity V, and C moves towards A with same velocity V. Then the velocity of centre of mass of the system of particles is
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
 .
.
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionA particle moves with initial velocity v0 and retardation αv, where v is velocity at any instant t. Then the particle
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionThe acceleration-time (a−t) graph of a particle moving along straight line is as shown in figure. The time at which velocity of particle becomes equal to its initial velocity is

View Solution
