Two masses m1 and m2 are suspended together by a massless spring of spring constant k as shown in figure. When the masses are in equilibrium , m1 is removed without the disturbing the system. Calculate the amplitude of oscillation and the angular frequency of m2.
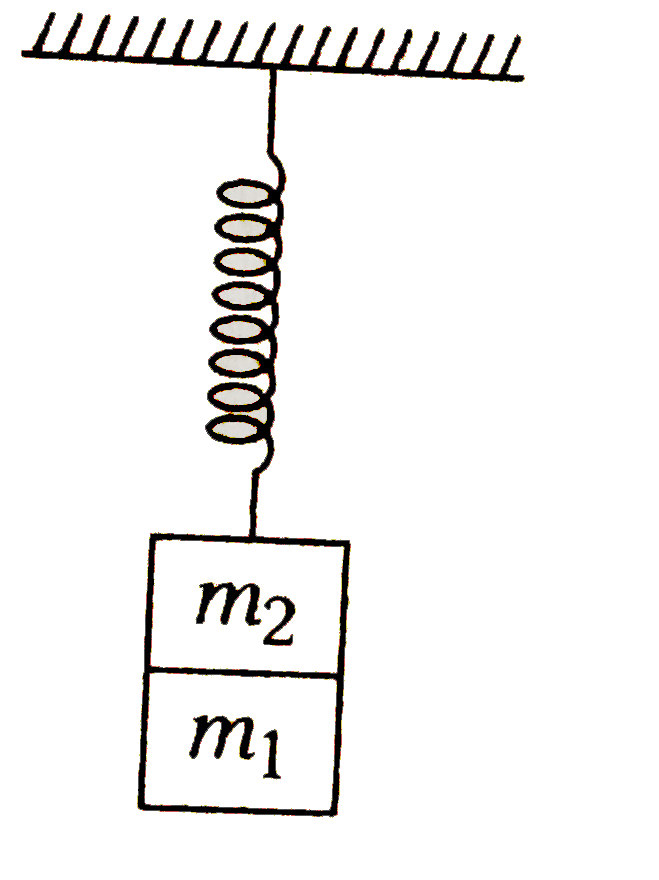
m1gk
m2gk
(m1+m2)gk
(m2−m1)gk
The correct Answer is:A
With mass m2 alone, the extension of the spring l is given as
m2g=kl
With mass (m1+m2), the extension l' is given by
(m1+m2)g=kl'=k(l+△l)
Hence △l is the amplitude of vibration.
subtracting Eq. (i) from Eq. (ii) we get m1g=k△l
or △l=m1gk
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Two masses m1=1kgandm2=0.5kg are suspended together by a massless spring of spring constant 12.5Nm−1. When masses are in equilibrium m1 is removed without disturbing the system. New amplitude of oscillation will be
View SolutionTwo masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000Nm−1 . When the masses are in equilibrium 8 kg is removed without disturbing the system . The amplitude of oscillation is
View Solution
Knowledge Check
Two masses m1andm2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is
A√(k/m1)B√(k/m2)C√[k(m1+m2)]D√[k/(m1m2)]
Two masses m1andm2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is
View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -
View SolutionTwo masses m 1 and m 2 are suspended together by a massless spring of constant K . When the masses are in equilibrium, m 1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo masses M and m are suspended together by massless spring of force constant -k. When the masses are in equilibrium, M is removed without disturbing the system. The amplitude of oscillations.
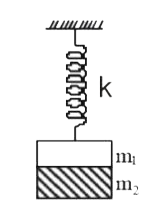
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View SolutionA body of mass 'm' hangs from three springs, each of spring constant 'k' as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period–
View SolutionA solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
View Solution
