Two moles of a diatomic ideal gas is taken through pT= constant. Its temperature is increased from T to 2T. Find the work done by the system?
The correct Answer is:D
To solve the problem of finding the work done by the system when two moles of a diatomic ideal gas are taken through a constant pT path while its temperature is increased from T to 2T, we can follow these steps:
1. Understand the Given Information:
- We have 2 moles of a diatomic ideal gas.
- The process is along a path where pT=constant.
- The initial temperature Ti=T and the final temperature Tf=2T.
2. Express the Constant:
- Let k=pT be the constant. Therefore, we can write:
p=kT
3. Use the Ideal Gas Law:
- According to the ideal gas law, we have:
pV=nRT
- Substituting p from the previous step:
kTV=nRT
- Rearranging gives:
V=nRT2k
4. Differentiate Volume with Respect to Temperature:
- Differentiate both sides with respect to T:
dV=ddT(nRT2k)
- This results in:
dV=2nRTkdT
5. Calculate Work Done:
- The work done W in a process can be expressed as:
W=∫PdV
- Substitute P=kT and dV=2nRTkdT:
W=∫kT(2nRTkdT)
- Simplifying gives:
W=2nR∫dT
6. Evaluate the Integral:
- The integral of dT from T to 2T is:
W=2nR(T)2TT=2nR(2T−T)=2nRT
7. Substitute the Number of Moles:
- Since n=2 (given in the problem):
W=2⋅2RT=4RT
Final Answer:
The work done by the system is:
4RT
- We have 2 moles of a diatomic ideal gas.
- The process is along a path where pT=constant.
- The initial temperature Ti=T and the final temperature Tf=2T.
- Let k=pT be the constant. Therefore, we can write:
p=kT
- According to the ideal gas law, we have:
pV=nRT
- Substituting p from the previous step:
kTV=nRT
- Rearranging gives:
V=nRT2k
- Differentiate both sides with respect to T:
dV=ddT(nRT2k)
- This results in:
dV=2nRTkdT
- The work done W in a process can be expressed as:
W=∫PdV
- Substitute P=kT and dV=2nRTkdT:
W=∫kT(2nRTkdT)
- Simplifying gives:
W=2nR∫dT
- The integral of dT from T to 2T is:
W=2nR(T)2TT=2nR(2T−T)=2nRT
- Since n=2 (given in the problem):
W=2⋅2RT=4RT
The work done by the system is:
4RT
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Exercise 21.1
1 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Exercise 21.2
7 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 3
1 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
In a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
View Solution(a) 2 moles of an ideas gas is heated at constant pressure so that its temperature increases from 27∘C to 127∘C. Find work done by the gas.
(b) In a process, the volume of gas increases from 1000 cc to 2000 cc at constant pressure 100 kPa. Find work done by the gas.
View Solution
Knowledge Check
In a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
A200 RB−200RC−100RD−400RTwo moles of an ideal diatomic gas is taken through a process VT2= constant so that its temperature increases by ΔT=300K. The ratio (ΔUΔQ) of increase in internal energy and heat supplied to the gas during the process is
A2B3C4D5When an ideal diatomic gas is heated at constant pressure, its intenal energy is increased by 50cal then the work done by the gas is
A30calB50calC70calD20cal
Two moles of an ideal monatomic gas is heated at constant pressure so that its temperature increases from 127∘C to 227∘C , then work done by gas
View Solutionn moles of an ideal gas is taken through a four step cyclic process as shown in the diagram. Calculate work done by the gas in a cycle in terms of temperatures T1,T2,T3 and T4
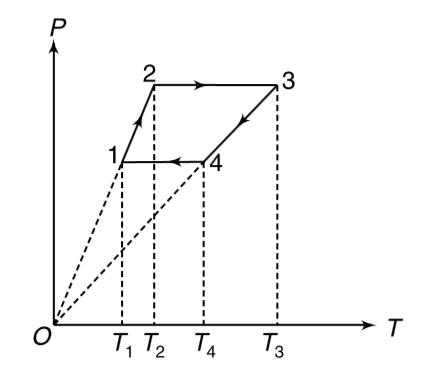
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
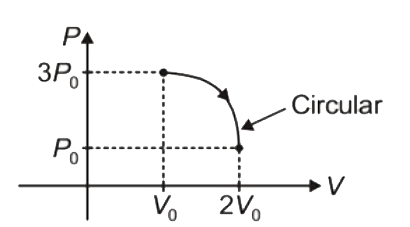
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View Solution
