Find the molar specific heat of the process p=aT for a monoatomic gas, a being constant.
The correct Answer is:B
To find the molar specific heat of the process defined by P=aT for a monoatomic gas, we can follow these steps:
Step 1: Define Molar Specific Heat
The molar specific heat C is defined as the amount of heat added per unit temperature change. Mathematically, it can be expressed as:
C=dQdT
Step 2: Apply the First Law of Thermodynamics
According to the first law of thermodynamics:
dU=dQ−dW
This can be rearranged to express dQ:
dQ=dU+dW
Step 3: Express dU for a Monoatomic Gas
For a monoatomic ideal gas, the change in internal energy dU is given by:
dU=nCVdT
For one mole of gas (n=1), this simplifies to:
dU=CVdT
Step 4: Express dW
The work done dW in a process can be expressed as:
dW=PdV
Step 5: Substitute dQ in Terms of dT
Substituting the expressions for dU and dW into the equation for dQ:
dQ=CVdT+PdV
Step 6: Differentiate with Respect to T
Now, we differentiate dQ with respect to T:
dQdT=CV+PdVdT
Thus, we have:
C=CV+PdVdT
Step 7: Relate P and V Using the Ideal Gas Law
Using the ideal gas law PV=nRT, for one mole (n=1):
P=RTV
Given P=aT, we can set these equal:
RTV=aT
From this, we can solve for V:
V=RT2a
Step 8: Differentiate V with Respect to T
Now, we differentiate V with respect to T:
dVdT=ddT(RT2a)=2RTa
Step 9: Substitute dVdT Back into the Equation for C
Substituting dVdT back into the equation for C:
C=CV+P(2RTa)
Step 10: Substitute P into the Equation
Substituting P=aT:
C=CV+aT⋅2RTa
This simplifies to:
C=CV+2R
Step 11: Calculate CV for a Monoatomic Gas
For a monoatomic gas, the molar specific heat at constant volume CV is:
CV=3R2
Step 12: Final Calculation
Substituting CV into the equation for C:
C=3R2+2R=3R2+4R2=7R2
Final Answer
Thus, the molar specific heat of the process P=aT for a monoatomic gas is:
C=7R2
The molar specific heat C is defined as the amount of heat added per unit temperature change. Mathematically, it can be expressed as:
C=dQdT
According to the first law of thermodynamics:
dU=dQ−dW
This can be rearranged to express dQ:
dQ=dU+dW
For a monoatomic ideal gas, the change in internal energy dU is given by:
dU=nCVdT
For one mole of gas (n=1), this simplifies to:
dU=CVdT
The work done dW in a process can be expressed as:
dW=PdV
Substituting the expressions for dU and dW into the equation for dQ:
dQ=CVdT+PdV
Now, we differentiate dQ with respect to T:
dQdT=CV+PdVdT
Thus, we have:
C=CV+PdVdT
Using the ideal gas law PV=nRT, for one mole (n=1):
P=RTV
Given P=aT, we can set these equal:
RTV=aT
From this, we can solve for V:
V=RT2a
Now, we differentiate V with respect to T:
dVdT=ddT(RT2a)=2RTa
Substituting dVdT back into the equation for C:
C=CV+P(2RTa)
Substituting P=aT:
C=CV+aT⋅2RTa
This simplifies to:
C=CV+2R
For a monoatomic gas, the molar specific heat at constant volume CV is:
CV=3R2
Substituting CV into the equation for C:
C=3R2+2R=3R2+4R2=7R2
Thus, the molar specific heat of the process P=aT for a monoatomic gas is:
C=7R2
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Exercise 21.11videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Exercise 21.27videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 31videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions10videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
Molar specific heat at constant volume Cv for a monatomic gas is
A32RB52RC3RD2R - Question 2 - Select One
Graph for specific heat at constant volume for a monoatomic gas
A B
B C
C D
D - Question 3 - Select One
One mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
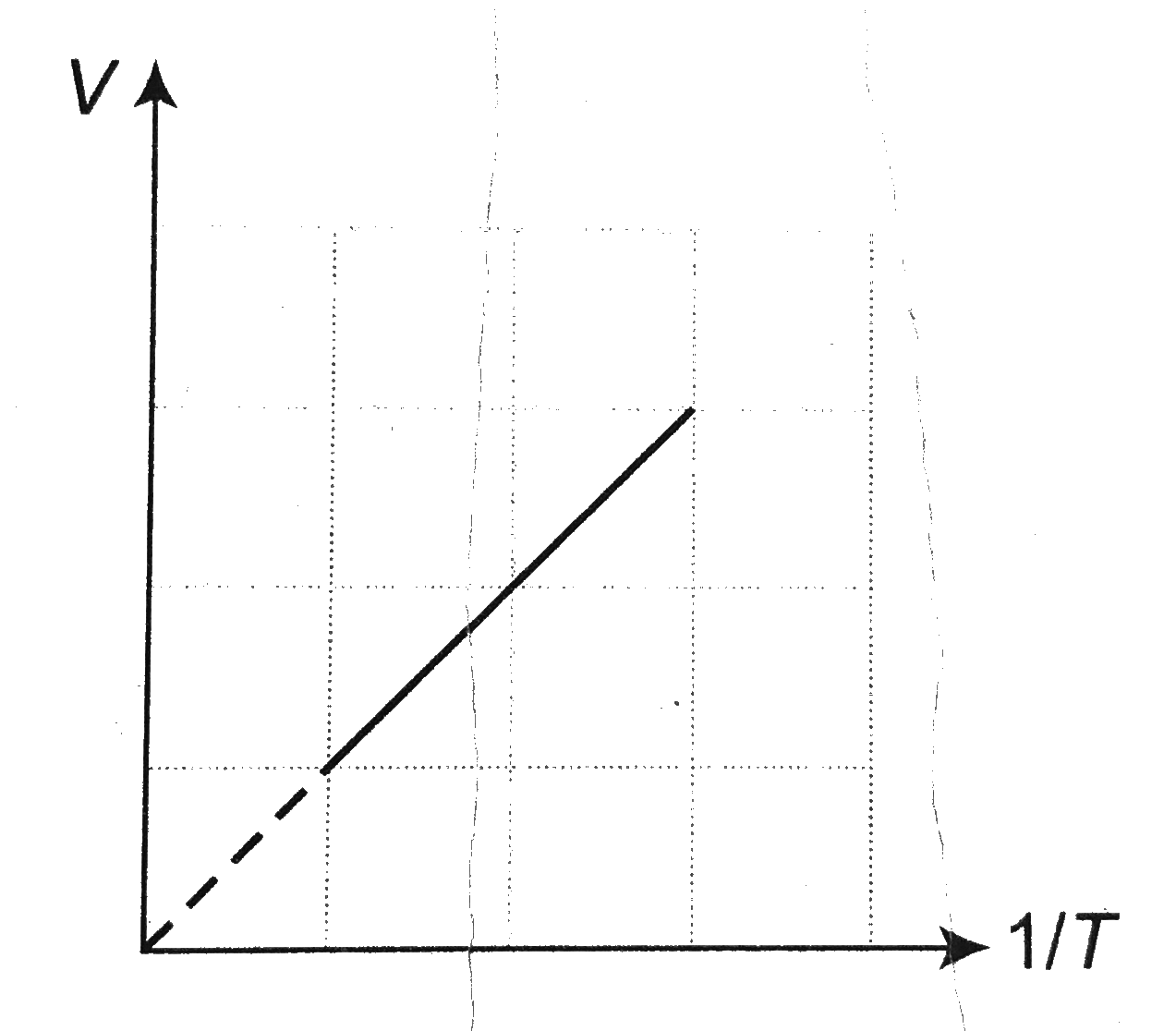
R is a gas constant.A3R4BR2CR3D2R3
[" A monoatomic ideal gas follows the process: "],[TV^(32)=" constant "],[" The molar specific heat for this process is "((5R)/(y))." Where "R" is gas constant.Find the value of "2y "]
View SolutionAn ideal gas is made to undergo a process T=T0eαV where T0 and α are constants. Find the molar specific heat capacity of the gas in the process if its molar specific heat capacity at constant volume is Cv. Express your answer as a function of volume (V).
View SolutionFind the molar specific heat of mixture at constnat volume. It one mole of a monoatomic gas is mixed with three moles of a diatomic gas.
View SolutionGraph for specific heat at constant volume for a monoatomic gas
View SolutionThe molar specific heat at constant volume, for a non linear triatomic gas is
View Solution

