Two non-conducting spheres of radii R1 and R2 and carrying uniform volume charge densities +ρ and −ρ, respectively, are placed such that they partially overlap, as shown in the figure. At all points in the overlapping region
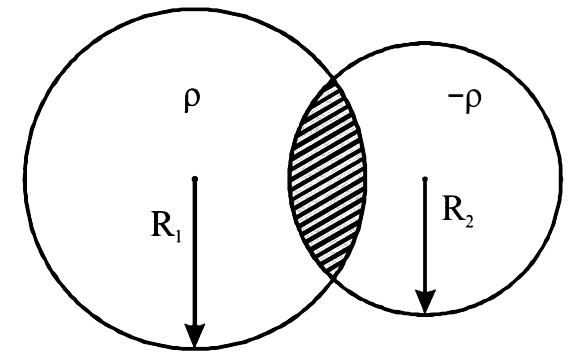
the electrostatic field is zero
the electrostatic potential is constant
the electrostatic field is constant in magnitude
the electrostatic field has same direction.
In triangle PC1C2,→r2=→d+→r1
The electrostatic field at point P is
→E=K(ρ43πR31)→r2R31+(K(ρ43πR32)→r1R32
=Kρ43π(→r2−→r1)=ρ3ε0→d
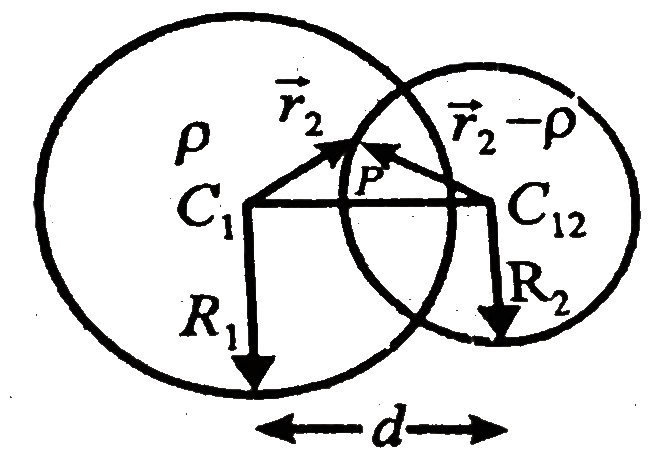
Similar Questions
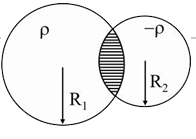
Two non-conducting spheres of radii R1 and R2 and carrying uniform volume charge densities +ρ and −ρ respectively are placed such that they partially overlapping region.
View SolutionThere is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View Solution
Knowledge Check
Two non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio ρ1ρ2 can be
A(a) −4B(b) −3325C(c) 3225D(d) 4Two conducting spheres of radii r1 and r2 are charged to the same surface charge density . The ratio of electric field near their surface is
Ar21/r22Br22/r21Cr1/r2D1:1Two conducting spheres of radii r1 and r2 are equally charged. The ratio of their potentral is-
Ar21/r22Br22/r21Cr1/r2Dr2/r1
Two charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionThere are two nonconducting spheres having uniform volume charge densities ρ and −ρ . Both spheres have equal radius R. The spheres are now laid down such that they overlap as shown in Fig.2.125. Take →d=O1−→O2.

The electric field →E in the overlapped region is
View SolutionThere are two nonconducting spheres having uniform volume charge densities ρ and −ρ . Both spheres have equal radius R. The spheres are now laid down such that they overlap as shown in Fig.2.125. Take →d=O1−→O2.

The potential difference ΔV between the centres of the two spheres for d=R is
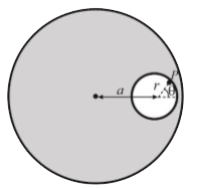
View SolutionA solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
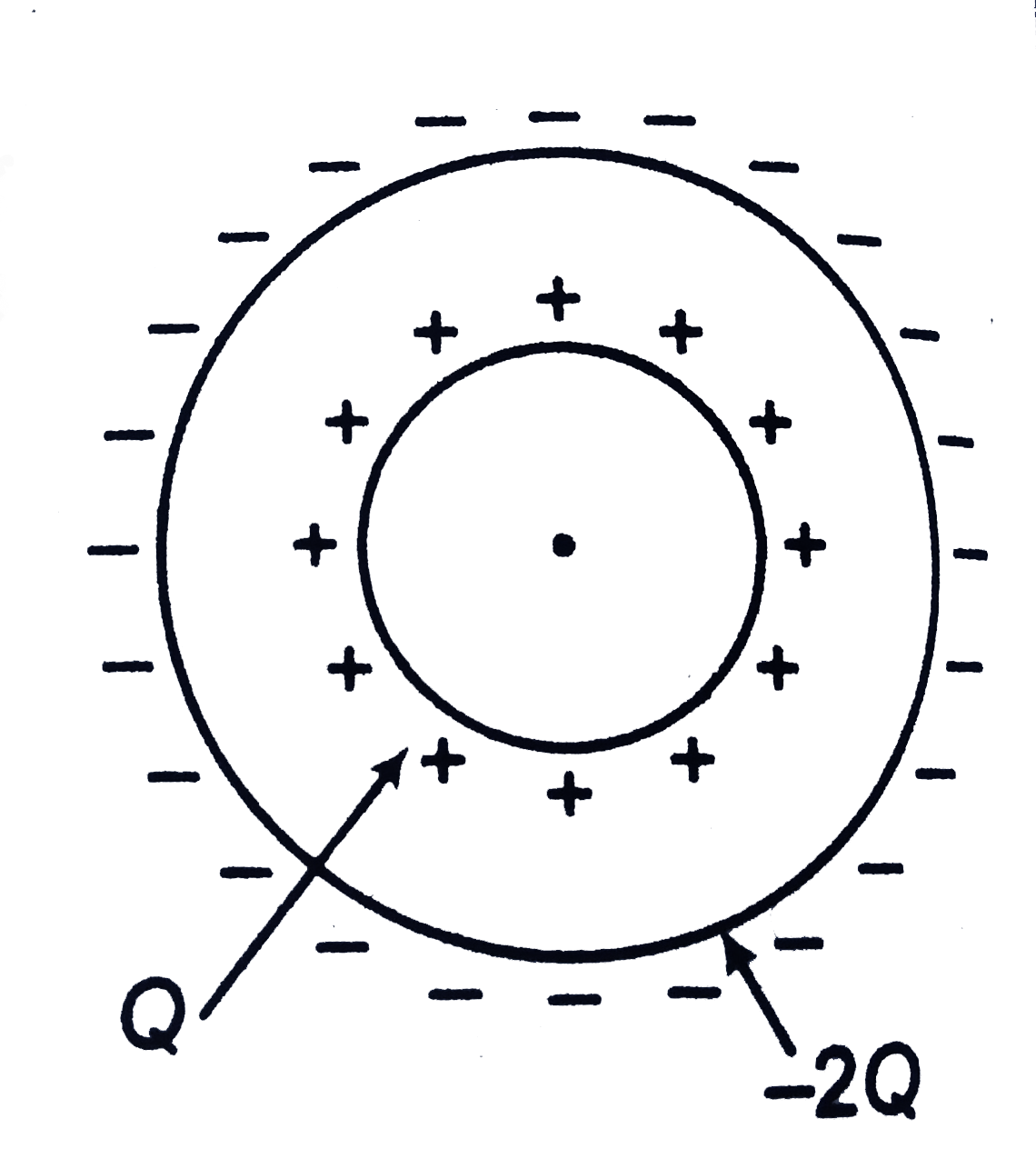
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View Solution
