Two paper screens A and B are separated by a distance of 200 m. A bullet pierces A and then B. The hole in B is 40 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is
200ms−1
400ms−1
600ms−1
700ms−1
The correct Answer is:D
To solve the problem, we need to determine the horizontal velocity of the bullet at the moment it hits screen A. We can break down the solution into several steps:
Step 1: Understand the Problem
We have two screens, A and B, separated by a distance of 200 m. The bullet travels horizontally and makes a hole in both screens. The hole in screen B is 40 cm (or 0.4 m) below the hole in screen A.
Step 2: Determine the Time of Flight
Since the bullet is traveling horizontally, we can use the horizontal distance to calculate the time it takes to travel from screen A to screen B. The distance between the screens is 200 m.
Using the formula:
Distance=Velocity×Time
Let u be the horizontal velocity of the bullet. The time t taken to travel from A to B can be expressed as:
t=200u
Step 3: Analyze the Vertical Motion
While the bullet is traveling horizontally, it is also falling due to gravity. The vertical distance fallen is 0.4 m. We can use the following kinematic equation for vertical motion:
s=ut+12at2
In this case, the initial vertical velocity u is 0 (since the bullet starts falling from rest), and the acceleration a is g=9.8m/s2. Thus, the equation simplifies to:
0.4=0+12⋅9.8⋅t2
Step 4: Substitute for Time
Now we substitute t=200u into the vertical motion equation:
0.4=12⋅9.8⋅(200u)2
Step 5: Solve for u
Rearranging the equation gives:
0.4=12⋅9.8⋅40000u2
Multiplying both sides by 2u2 gives:
0.8u2=9.8⋅40000
u2=9.8⋅400000.8
Calculating the right side:
u2=3920000.8=490000
Taking the square root:
u=√490000≈700m/s
Final Answer
The velocity of the bullet at screen A is approximately 700m/s.
---
We have two screens, A and B, separated by a distance of 200 m. The bullet travels horizontally and makes a hole in both screens. The hole in screen B is 40 cm (or 0.4 m) below the hole in screen A.
Since the bullet is traveling horizontally, we can use the horizontal distance to calculate the time it takes to travel from screen A to screen B. The distance between the screens is 200 m.
Distance=Velocity×Time
Let u be the horizontal velocity of the bullet. The time t taken to travel from A to B can be expressed as:
t=200u
While the bullet is traveling horizontally, it is also falling due to gravity. The vertical distance fallen is 0.4 m. We can use the following kinematic equation for vertical motion:
s=ut+12at2
In this case, the initial vertical velocity u is 0 (since the bullet starts falling from rest), and the acceleration a is g=9.8m/s2. Thus, the equation simplifies to:
0.4=0+12⋅9.8⋅t2
Now we substitute t=200u into the vertical motion equation:
0.4=12⋅9.8⋅(200u)2
Rearranging the equation gives:
0.4=12⋅9.8⋅40000u2
Multiplying both sides by 2u2 gives:
0.8u2=9.8⋅40000
u2=9.8⋅400000.8
Calculating the right side:
u2=3920000.8=490000
Taking the square root:
u=√490000≈700m/s
The velocity of the bullet at screen A is approximately 700m/s.
Topper's Solved these Questions
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (UNIFORM CIRCULAR MOTION)
8 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - CHECK YOUR NEET VITALS
22 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (MOTION IN A PLANE )
23 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS
32 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
Similar Questions
Two paper screens A and B are separated by a distance of 100m. A bullet pierces A and B. The hole in B is 10cm below the hole in A. If the bullet is travelling horizontally at the time of hitting the screen A, calculate the velocity of the bullet when it hits the screen A. Neglect resistance of paper and air.
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
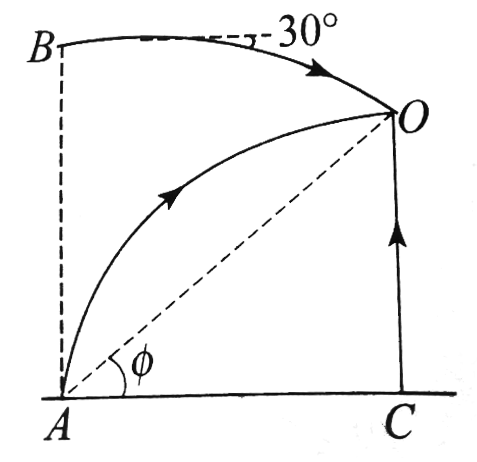
Find the time in which bullets will collide (seconds ):
View Solution
Knowledge Check
Two paper screens A and B are separated by 150m. A bullet pierces A and B. The hole in B in 15 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is: (g=10ms−2)
A100√3ms−1B200√3ms−1C300√3ms−1D500√3ms−1Two paper screens A and B are separated by distance 100 m. A bullet penetrates A and B, at points P and Q respectively, where Q is 10 cm below P. If bullet is travelling horizotally at the time of hitting A, the velocity of bullet at A is nearly
A100 m/sB200 m/sC600 m/sD700 m/sTwo thin wood screens A and B are separated by 200m a bullet travelling horizontally at speed of 600m/s hits the screen A penetrates through it and finally emerges out from B making holes in A and B the resistance of air and wood are negligible the difference of heights of the holes in A and B is.
A5mB4990mC7√90mDzero
Points A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
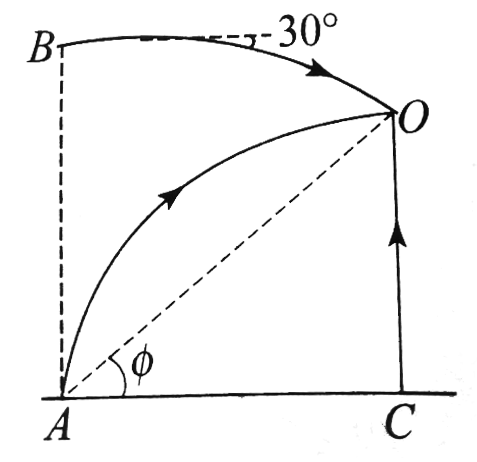
Find the velocity of bullet at A:
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.

Find the elevation angle ∠θ=∠OAC:
View SolutionTwo wooden blocks of masses 1kg and 2kg are separated by a certain distance A bullet of mass 50g fired from a gun pierces through the block of mass 1kg and then stopped in the second block After the impact of the bullet both blocks start moving with the same speed Calculate the percentage loss in the initial velocity of the bullet when it is inbetween the two blocks .
View SolutionTo understand the effect of air resistance on the motion of a bullet let's consider a bullet of the shape shown in the fig. The bullet is flying horizontally. The cross section of cylindrical part is A and the conical part has a semi vertical angle of 45∘. Assume that the bullet is fired with initial velocity u and moves in a gaseous medium in which molecules are at rest (do you think this assumption is necessary?). Collisions of the molecules with the bullet are elastic. Take mass of bullet to be M, density of gaseous medium as ρ and disregard gravity.
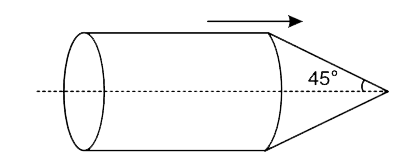
(a) Consider two bullets one small and other large, made of same material. Which will experience larger retardation due to air resistance ?
(b) Write the speed of bullet after time t
(c) Write distance travelled by the bullet in time t.
View SolutionA bullet of mass a and velocity b is fired into a large block of mass c. the final velocity of the system is
View Solution
