Two particale of same mass and charge throw in same direction along the horizonal with same velocity v from two didffent heights h1 and h2 (h1<h2). Initially they were located in the same vertical line. Select the corredct alternative (s).
Both the particles always lie on a vertical line
Acceleration of the centre of mass of the two particles is g downwards
Horizontal dosplacement on reaching to ground of particle lying at h1 is less than the value, which would had been in the absence of charges on them
Horizontal displacement on reaching to ground of particle lying at h2 is more than the value, which would had been in the absence of charges on them
To solve the problem, we need to analyze the motion of the two particles that are thrown horizontally from different heights. Let's break down the solution step by step:
Step 1: Understand the Initial Conditions
- We have two particles, both with the same mass (m) and the same charge (q).
- They are thrown horizontally with the same initial velocity (v).
- The particles are released from different heights: h1 and h2 (where h1<h2).
- Initially, they are aligned vertically.
Step 2: Analyze the Motion of Each Particle
- Since both particles are thrown horizontally, their horizontal motion will be uniform because there are no horizontal forces acting on them (ignoring air resistance).
- The vertical motion of each particle is influenced by gravity. The only force acting on them in the vertical direction is the gravitational force, which causes them to accelerate downwards at g (acceleration due to gravity).
Step 3: Determine the Time of Flight
- The time it takes for each particle to reach the ground can be calculated using the formula for free fall:
t=√2hg
- For particle 1 (height h1):
t1=√2h1g
- For particle 2 (height h2):
t2=√2h2g
Step 4: Compare the Times of Flight
- Since h1<h2, it follows that:
t1<t2
- This means particle 1 will hit the ground before particle 2.
Step 5: Analyze Horizontal Displacement
- The horizontal displacement for each particle can be calculated as:
x=v⋅t
- For particle 1:
x1=v⋅t1
- For particle 2:
x2=v⋅t2
Step 6: Conclusion
- Since t1<t2, it follows that:
x1<x2
- Therefore, when both particles reach the ground, particle 1 will be closer to the starting vertical line than particle 2.
Final Answer
- The correct alternative is that the particle thrown from the lower height (h1) will reach the ground first and will be closer to the starting vertical line than the particle thrown from the higher height (h2).
---
- We have two particles, both with the same mass (m) and the same charge (q).
- They are thrown horizontally with the same initial velocity (v).
- The particles are released from different heights: h1 and h2 (where h1<h2).
- Initially, they are aligned vertically.
- Since both particles are thrown horizontally, their horizontal motion will be uniform because there are no horizontal forces acting on them (ignoring air resistance).
- The vertical motion of each particle is influenced by gravity. The only force acting on them in the vertical direction is the gravitational force, which causes them to accelerate downwards at g (acceleration due to gravity).
- The time it takes for each particle to reach the ground can be calculated using the formula for free fall:
t=√2hg
- For particle 1 (height h1):
t1=√2h1g
- For particle 2 (height h2):
t2=√2h2g
- Since h1<h2, it follows that:
t1<t2
- This means particle 1 will hit the ground before particle 2.
- The horizontal displacement for each particle can be calculated as:
x=v⋅t
- For particle 1:
x1=v⋅t1
- For particle 2:
x2=v⋅t2
- Since t1<t2, it follows that:
x1<x2
- Therefore, when both particles reach the ground, particle 1 will be closer to the starting vertical line than particle 2.
- The correct alternative is that the particle thrown from the lower height (h1) will reach the ground first and will be closer to the starting vertical line than the particle thrown from the higher height (h2).
Similar Questions
Equal volumes of a liquid are poured in the three vessels A,B and C(h1<h2<h3). All the vessels have the same base area. Select the correct alternatives.
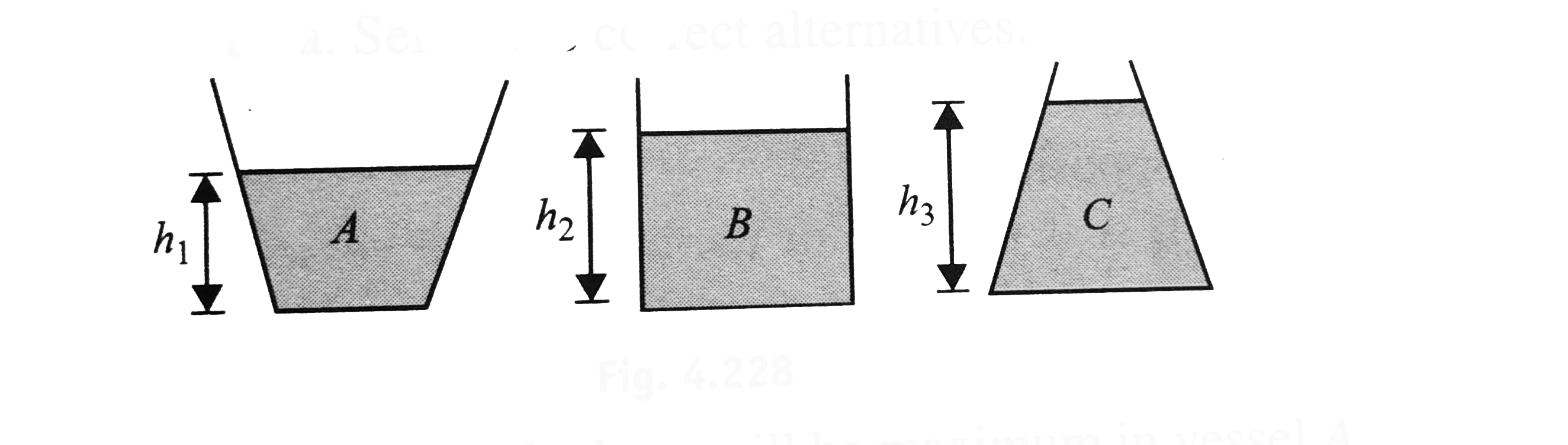
View SolutionEqual volumes of a liquid are poured in the three vessels A,B and C(h1<h2<h3). All the vessels have the same base area. Select the correct alternatives.

View SolutionTwo small balls having the same mass and charge and located on the same vertical at heights h1 and h2 are thrown in the same direction along the horizontal at the same velocity v. The first vall touches the ground at a horizontal distance R from the initial vertical position. At waht heigth h2 will the second ball be at this instant? Neglect any frictional resistance of air and the effect of any induced charge on the ground.
View SolutionTwo vessels A and B have same base area. Equal volumes of a liquid are poured in the two vessel to different heights hA and hB(hB>hA). In which vessel, the force on the base of vessel will be more?
View SolutionTwo masses m1 and m2(m1>m2) are falling from the same height when same air resistance acts on them
View SolutionTwo identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
View SolutionTwo stones are thrown with same speed u at different angles from ground n air if both stones have same range and height attained by them are h1andh2, then h1+h2 is equal to
View SolutionTwo capacitors C1 and C2 are charged to same potential V, but with opposite polarity as shown in the figure. The switches S1 and S2 are then closed

View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionA body projected horizontally with a velocityv from a height h has a range R.With what velocity a body is to be projected horizontally from a height h/2 to have the same range ?
View Solution
