Two particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
To solve the problem of finding the separation between two particles thrown horizontally in opposite directions when their velocities are perpendicular to each other, we can follow these steps:
1. Understanding the Problem:
Two particles are thrown horizontally from the same height h with velocities vA=4m/s to the left and vB=3m/s to the right. We need to find the separation between them when their velocity vectors are perpendicular.
2. Velocity Components:
The velocity of particle A can be represented as:
→VA=−4^i−gt^j
The velocity of particle B can be represented as:
→VB=3^i−gt^j
Here, g is the acceleration due to gravity, acting downwards.
3. Condition for Perpendicular Velocities:
The velocities are perpendicular when their dot product is zero:
→VA⋅→VB=0
Substituting the expressions for →VA and →VB:
(−4^i−gt^j)⋅(3^i−gt^j)=0
Expanding the dot product:
−12+g2t2=0
Rearranging gives:
g2t2=12
Thus,
t2=12g2
Taking the square root:
t=√12g
4. Substituting g:
Assuming g=10m/s2:
t=√1210=2√310=0.35s
5. Calculating Distances:
Now, we calculate the horizontal distances traveled by both particles at time t:
- For particle A:
xA=vA⋅t=4⋅0.35=1.4m
- For particle B:
xB=vB⋅t=3⋅0.35=1.05m
6. Total Separation:
The total separation S between the two particles when their velocities are perpendicular is:
S=xA+xB=1.4+1.05=2.45m
Final Answer:
The separation between the two particles when their velocities are perpendicular to each other is 2.45 meters.
Two particles are thrown horizontally from the same height h with velocities vA=4m/s to the left and vB=3m/s to the right. We need to find the separation between them when their velocity vectors are perpendicular.
The velocity of particle A can be represented as:
→VA=−4^i−gt^j
The velocity of particle B can be represented as:
→VB=3^i−gt^j
Here, g is the acceleration due to gravity, acting downwards.
The velocities are perpendicular when their dot product is zero:
→VA⋅→VB=0
Substituting the expressions for →VA and →VB:
(−4^i−gt^j)⋅(3^i−gt^j)=0
Expanding the dot product:
−12+g2t2=0
Rearranging gives:
g2t2=12
Thus,
t2=12g2
Taking the square root:
t=√12g
Assuming g=10m/s2:
t=√1210=2√310=0.35s
Now, we calculate the horizontal distances traveled by both particles at time t:
- For particle A:
xA=vA⋅t=4⋅0.35=1.4m
- For particle B:
xB=vB⋅t=3⋅0.35=1.05m
The total separation S between the two particles when their velocities are perpendicular is:
S=xA+xB=1.4+1.05=2.45m
The separation between the two particles when their velocities are perpendicular to each other is 2.45 meters.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - SOLVED EXAMPLES20videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - PRACTICE EXERCISE80videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE52videos
MOTION IN A STRAIGHT LINE & PLANE
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ2videos
Motion in Two Dimensions
Similar Questions
From a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The horizontal distance between two bodies, when their velocity are perpendicular to each other, is.View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
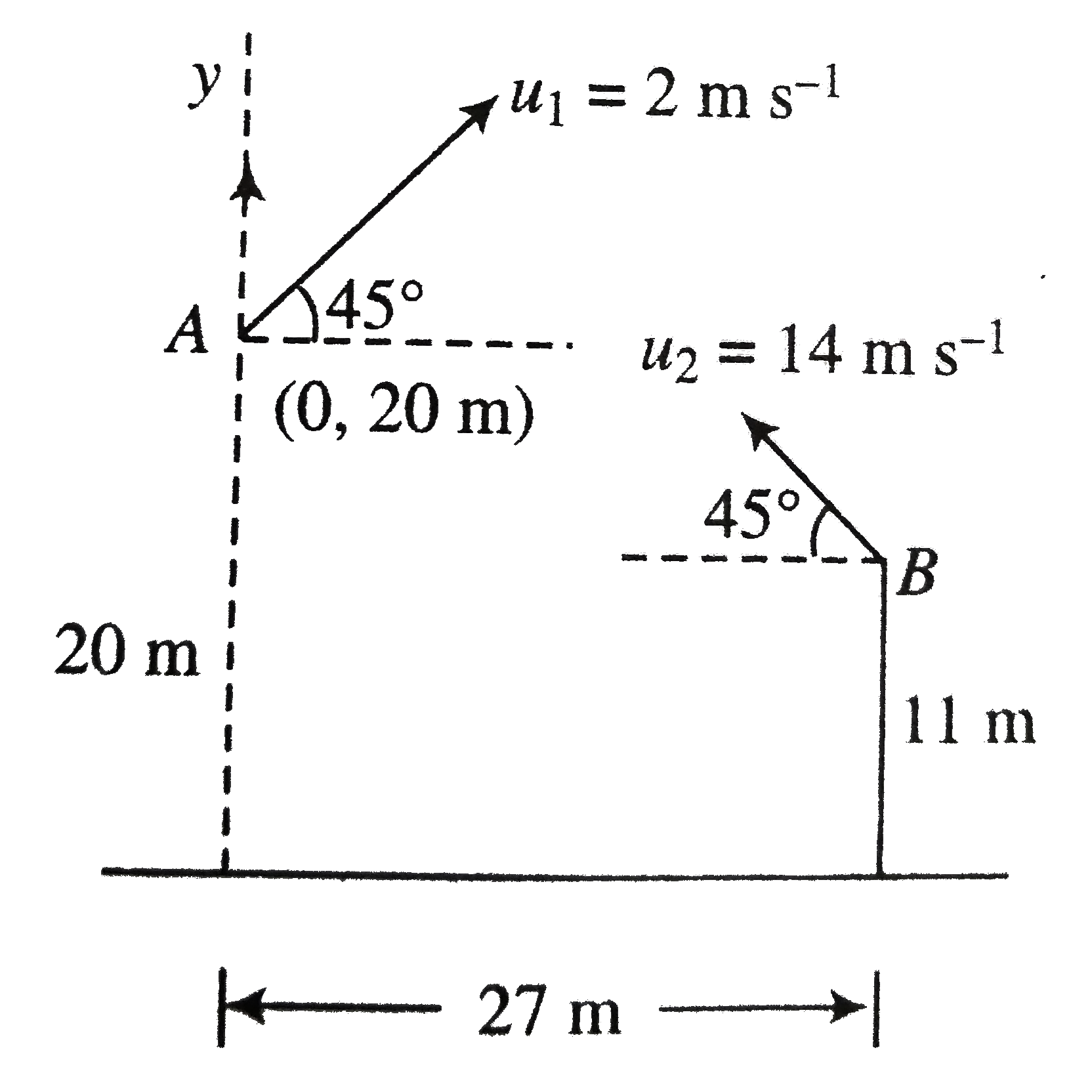
Minimum separation between A and B isView SolutionFrom a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The time taken for the velocity vectors of two bodies to become perpendicular to each other is :View SolutionFrom a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The time taken for the displacement vectors of two bodies to be come perpendicular to each other is.View SolutionTwo particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
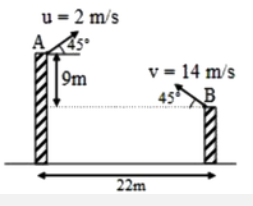 View Solution
View SolutionTwo particles are thrown horizontally in opposite directions with velocities u and 2u from the top of a high tower. The time after which their radius of curvature will be mutually perpendicular is
View SolutionFind the velocity of image,when object and mirror both are moving towards each other with velocities 4ms−1and5ms−1 respectively, is
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
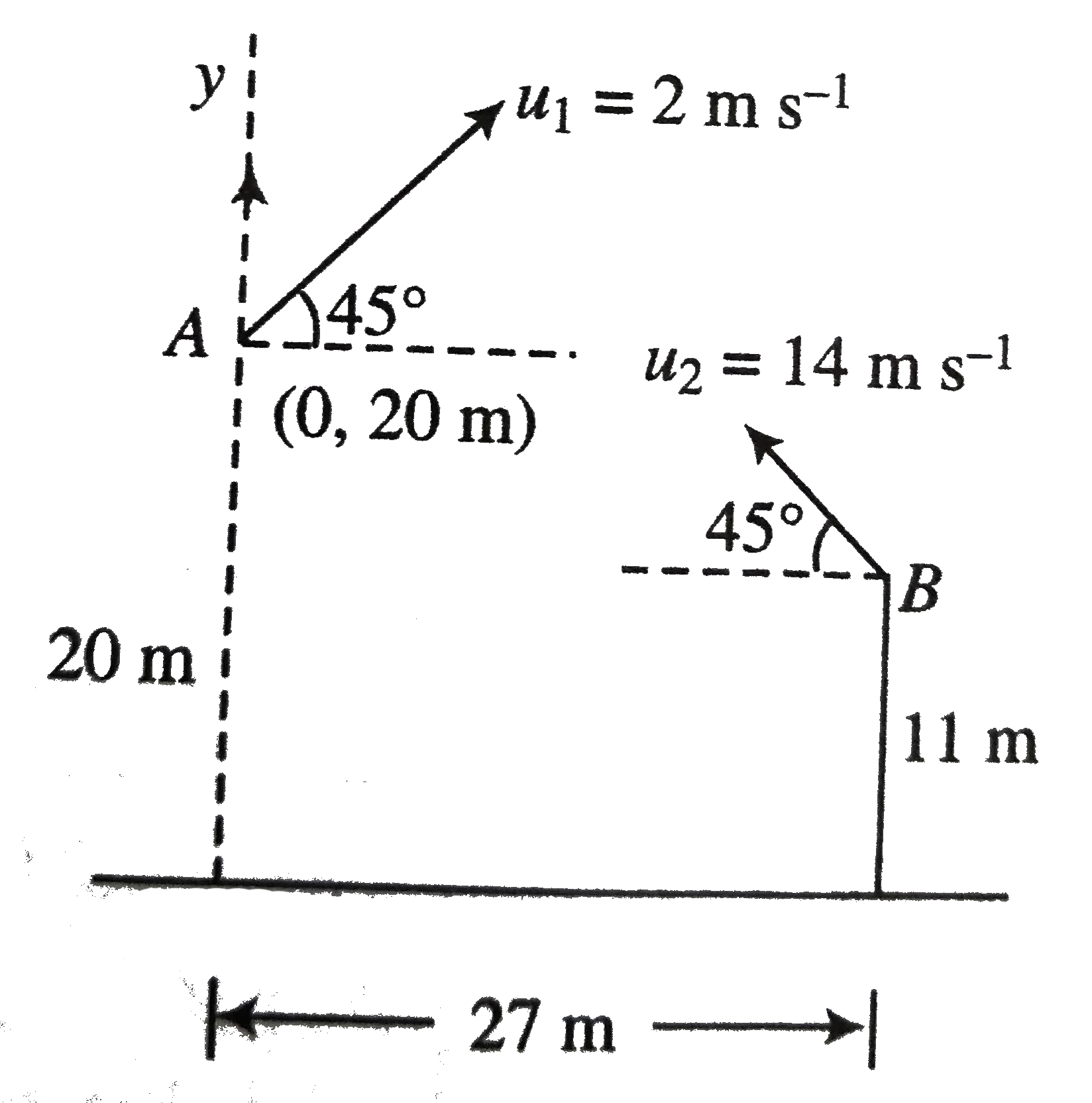
The relative velocity of B as seen from A inView SolutionTwo spheres of masses 4 kg and 8 kg are moving with velocities 2ms−1and3ms−1 away from each other along the same line. The velocity of centre of mass is
View Solution

