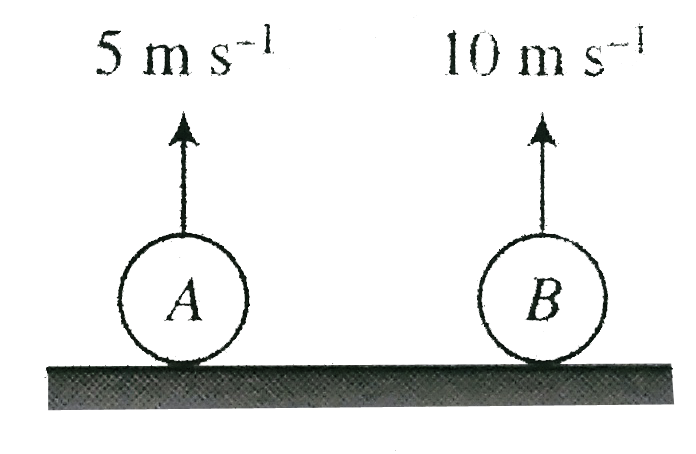
Two particles and are thown vertically upward with velocity, vertically upward with velocity, and respectively (g=10 m s^(-2)), Find separation between them after .
 .
.
Method -1: Position of aftre s
i.e., the particle will return to ground at
Hence, separation between and ,
Method-2: Relative velocity method:
Hence, relative separation between particles
becuase Distance between and after .
 .
.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
Knowledge Check
If a ball is thrown vertically upwards with a velocity of 40m/s, then velocity of the ball after 2s will be (g=10m/s2)
A15m/sB20m/sC25m/sD28m/sFind the maximum height reached by a particle which is thrown vertically upwards with the velocity of 20m/s (take g=10m/s2).
A40 mB10 mC20 mDzeroA ball is thrown vertically upward with a velocity of 20 m/s . After 3s , the magnitude of its displacement is (take g = 10 m/s2)
A15 mB25 mC10 mD20 m
A particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View SolutionTwo particles projected vertically upward from points (0,0) and (1,0)m with uniform velocity 10m/s and vm/s respectively, as shown in the figure. It is found that they collide after time t in space. Time t is 15(√x−1). Calculate x
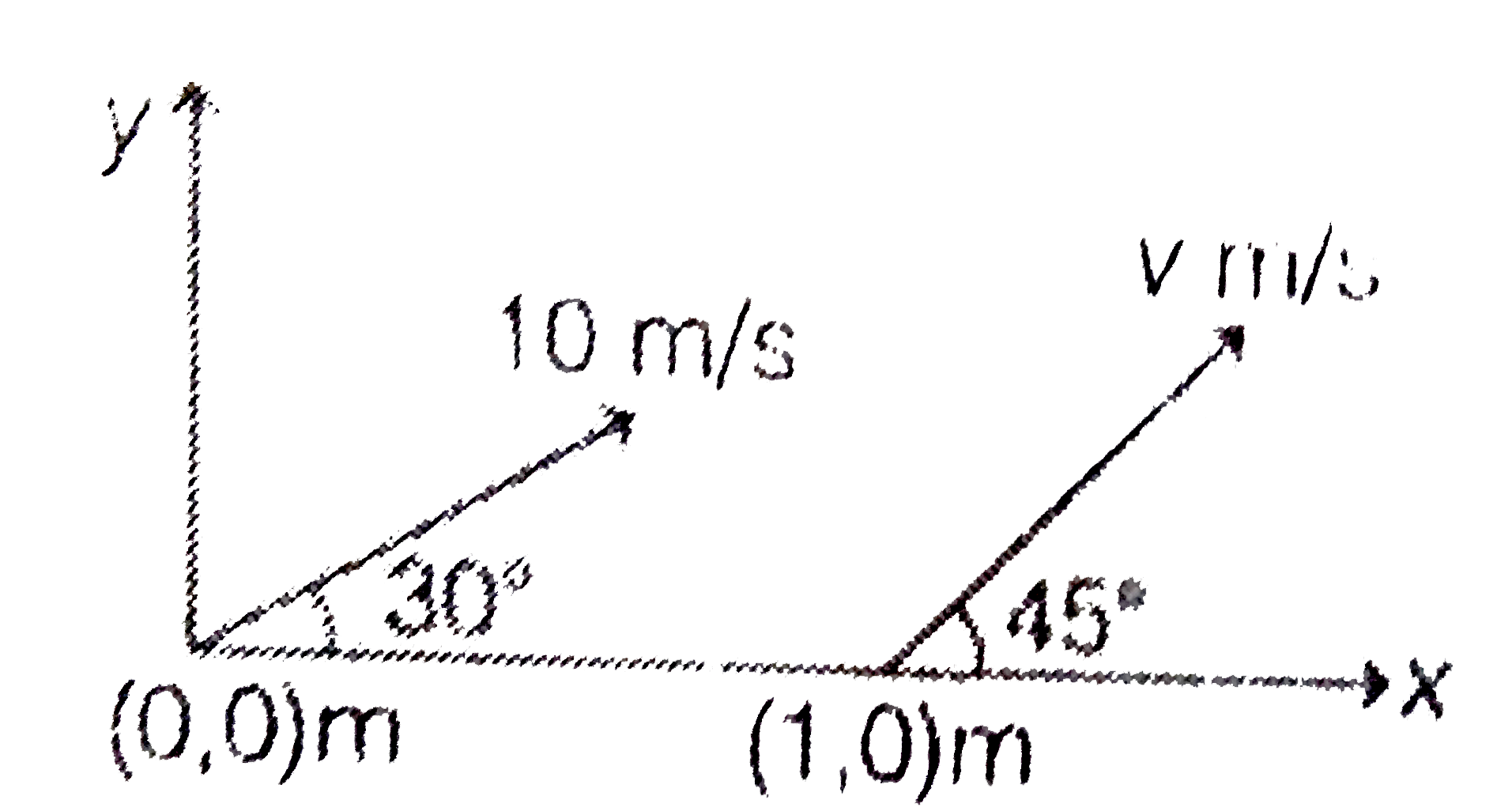
View SolutionA ball thrown vertically upwards with an initial velocity of 1.4m/s. The total displcement of the ball is
View SolutionTwo particles A and B are projected simultaneously in the direction shown in the figure with velocities VA=20m/s and VB=10m/s respectively. If they collide in air after 1/2 sec. then

View SolutionA stone of 200g is thrown vertically upward at a velocity of 60m/s. The kientic energy of the stone after 7s will be (g=10m/s2)
View Solution
