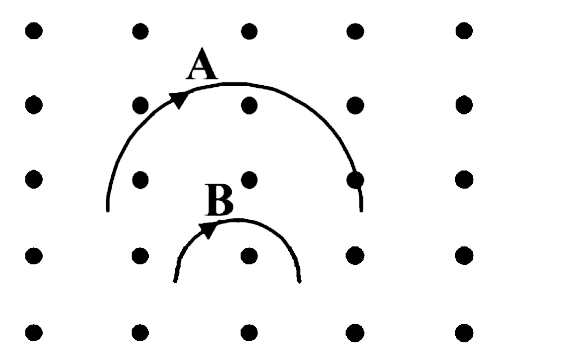
Two particles $A and B$ of masses $m_{A} and m_{B}$ respectively and having the same charge are moving in a plane . The speeds of the particles are $v_{A} and v_{B}$ respectively and the trajectories are as shown in the figure. Then

A

$m_{A} V_{A} < m_{B} v_{B}$

B

$m_{A} V_{A} > m_{B} v_{B}$

C

$m_{A} < m_{B}$ and $v_{A} < v_{B}$

D

$m_{A} = m_{B}$ and $v_{A} = v_{B}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$r = \frac{m v}{q B} \Rightarrow r \propto m v$ ( $q$ and $B$ are constant)
$∵ r_{A} > r_{B} \Rightarrow m_{A} V_{A} > m_{B} v_{B}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two particle A and B of masses $m_{A}$ and $m_{B}$ respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are $v_{A}$ and $v_{B}$ respectively and the trajectories are as shown in the figure. Then-

A $m_{A} v_{A} < m_{B} v_{B}$
B $m_{A} v_{A} > m_{B} v_{B}$
C $m_{A} < m_{B} and v_{A} < v_{B}$
D $m_{A} = m_{B} and v_{A} = v_{B}$
Question 2 - Select One
Two particles A and B of masses $m_{A} and m_{B}$ respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are $v_{A} and v_{B}$ respectively and the trajectories are as shown in the figure. Then -

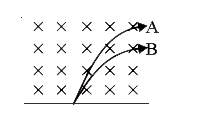A $m_{A} v_{A} < m_{B} v_{B}$
B $m_{A} v_{A} > m_{B} v_{B}$
C $m_{A} < m_{B} and v_{A} < v_{B}$
D $m_{A} = m_{B} and v_{A} = v_{B}$
Question 3 - Select One
Two particles $A$ and $B$ of masses $m_{A}$ and $m_{B}$ respectively and having the same charge are moving ina plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are $v_{A}$ and $v_{B}$ respectively and the trajectories are as shown in the figure. Then,

A $m_{A} v_{A} < m_{B} v_{B}$
B $m_{A} v_{A} > m_{B} v_{B}$
C $m_{A} < m_{B} and v_{A} < v_{B}$
D $m_{A} = m_{B} and v_{A} = v_{B}$

A2Z-SOURCE AND EFFECT OF MAGNETIC FIELD-AIIMS Questions

Home
Ask Doubt
Profile