Two particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
In relative motion, observer consioders himself at rest and observes the motiob of object. Graphically, we can draw the direction of motion of particle 2 w.r.t. particle 1 (Fig. 5.123). Both the particles are moving in gravitation field with same acceleration g. Hence, relative acceleration of particle 2 as seen from particle 1 will be zero. It means the relative velocity of the particle 2 w.r.t. particle 1 will be constant and will be equal to initial relative velocity. Graphically, we can draw the situation as shown in (Fig. 5.123).
AN is the minimum separation between the particles and BN is the relative separation between the particles when the distance between 1and2 is shortest. From figure, we can write
v12cosθ=14cos45∘+2cos45∘ ...(i)
v12sinθ=14sin45∘−2sin45∘ ....(ii)
From (i) and (ii), v12=10√2ms−1
cosθ=45andsinθ=35,asθ=37∘
Hence, minimum separation between the particles
=AN=ABsinθ=60×35=36m
The time when separation between the particles is minimum,
t=BN|→v12|=t=60cos37∘10√2=12√25s.
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples7videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.115videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
Two particles A and B are thown vertically upward with velocity, vertically upward with velocity, 5ms−1 and 10ms−1 respectively (g=10 m s^(-2)), Find separation between them after 1s.
 .View Solution
.View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View Solution
Knowledge Check
- Question 1 - Select One
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
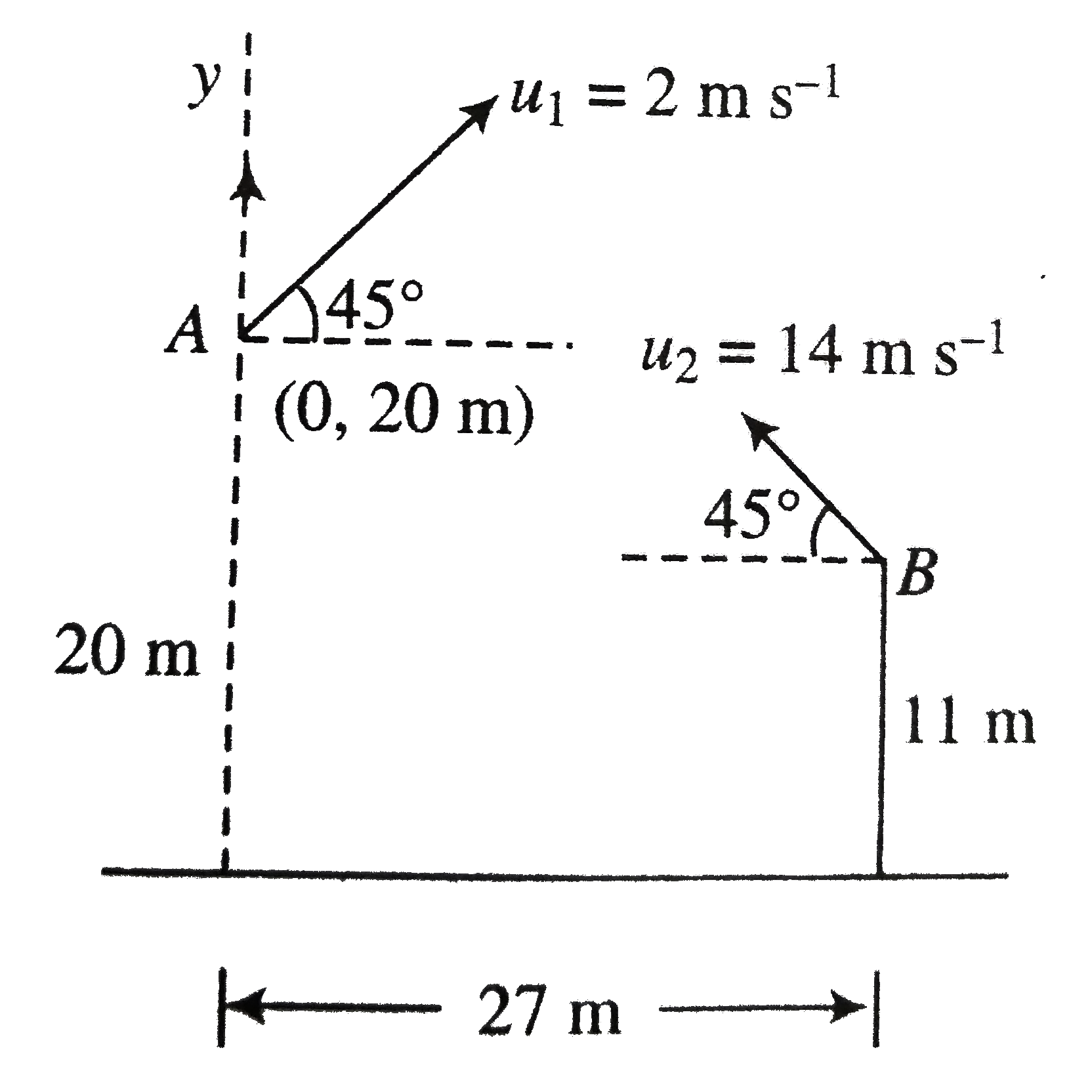
Minimum separation between A and B isA3 mB6 mC12 mD9 m - Question 2 - Select One
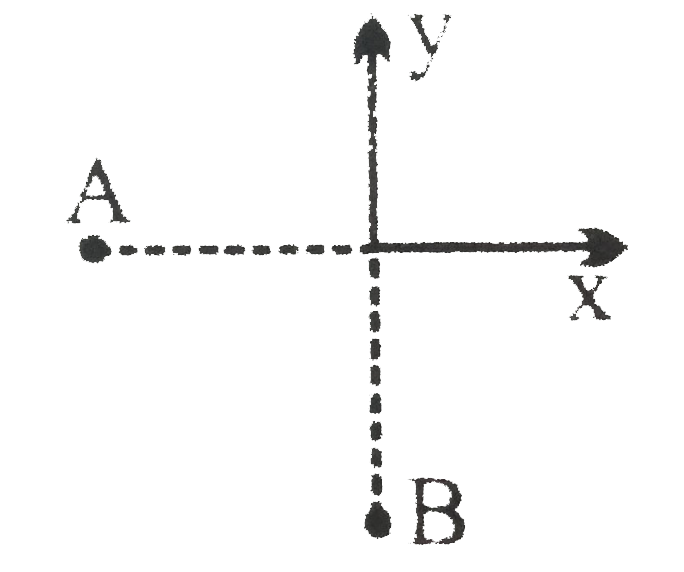
Particles A and B are moving with constant velocities along x and y axis respectively, the graph of separation between them with time is
 A
A B
B C
C D
D
- Question 3 - Select One
From a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The horizontal distance between two bodies, when their velocity are perpendicular to each other, is.A1 mB0.5 mC2 mD4 m
A particle is projected from an inclined plane OP1 from A with velocity v1=8ms−1 at an angle 60∘ with horizontal. An another particle is projected at the same instant from B with velocity v2=16ms−1 and perpendicular to the plane OP2 as shown in figure. After time 10(√3) s there separation was minimum and found to be 70m. Then find distance AB.
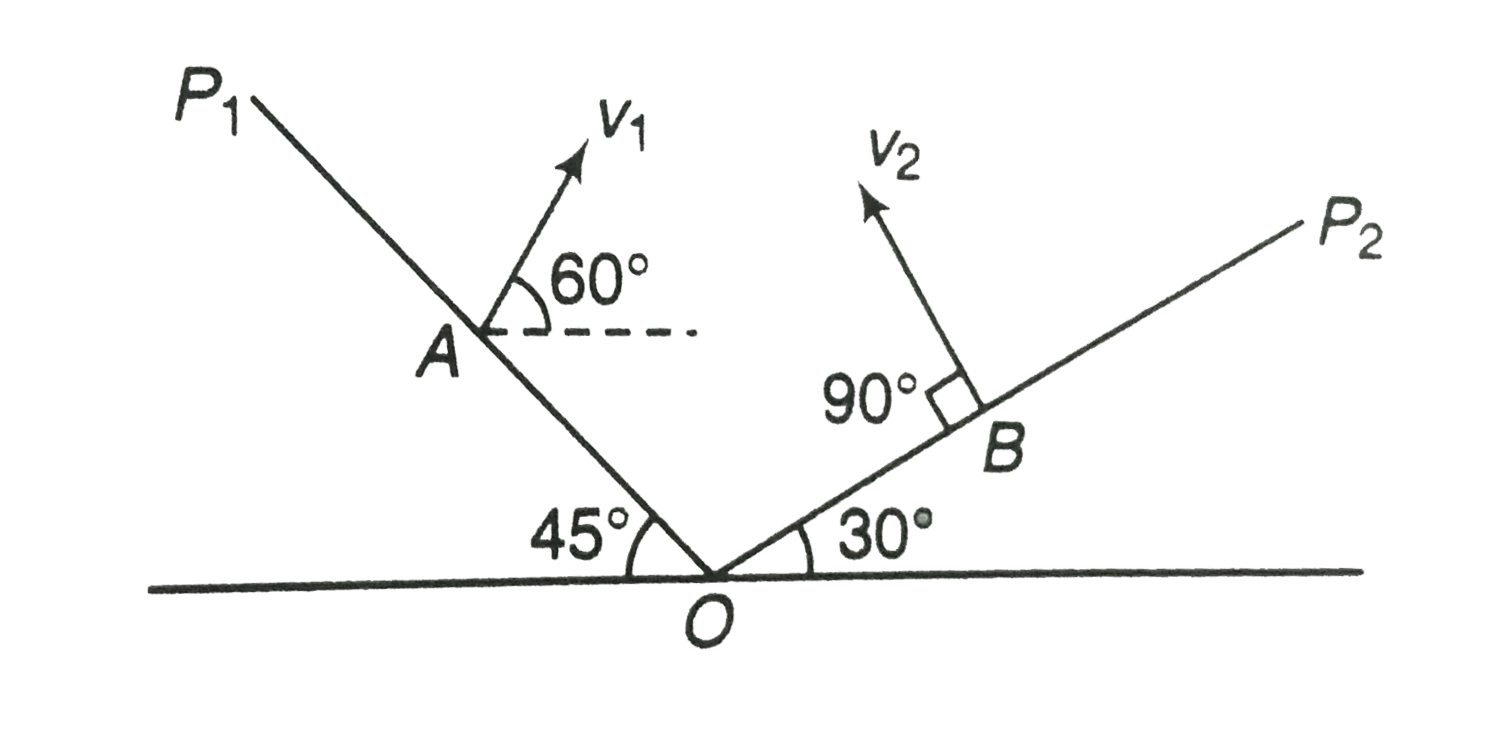 View Solution
View SolutionIn the figure shown in text, m1=m, m2=2m and initial distance between them is r0. Find velocities of the masses when separation between them becoms r02.
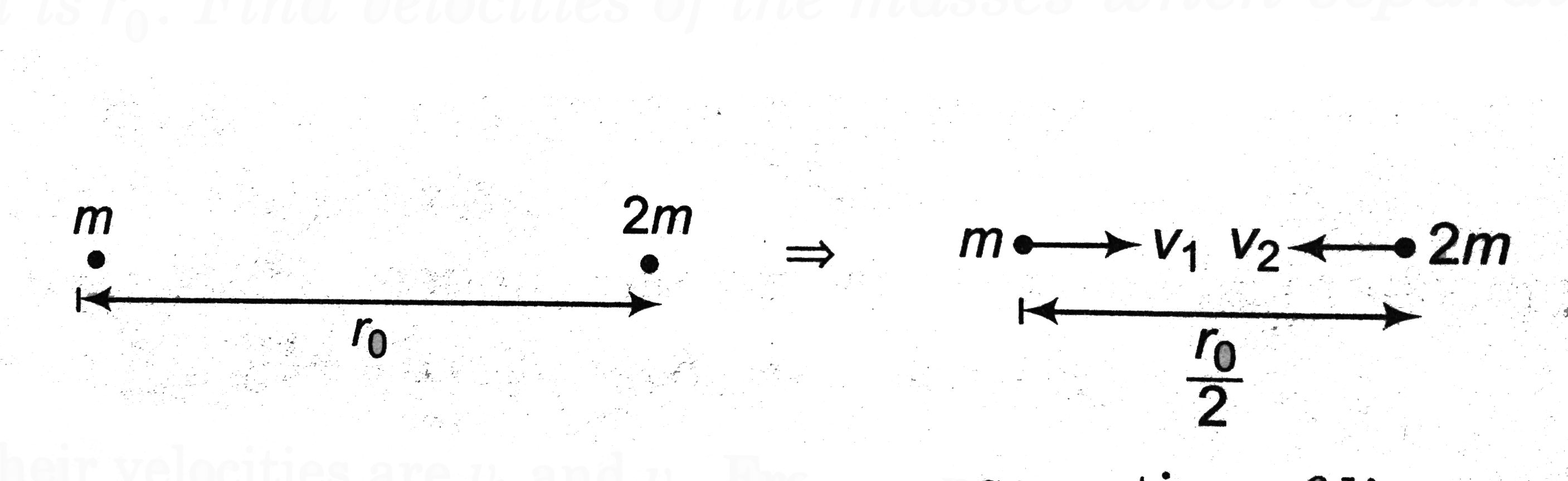 View Solution
View SolutionTwo bodies A and B are at position (2,3)m amd (5,7)m respectively. These two are moving with constant velocity 3ms−1 along −ve y axis and 4ms−1 along +ve x axis respectively. Minimum separation between them during their motion is
View SolutionTwo particles are projected from two points 4m apart on the horizontal ground, simultaneously with speed 20ms−1 above 60∘ and 15ms−1 above 30∘ from horizontal towards each other. Find the shortest distance between them during the flight.
View SolutionInitially two particles A and B are present at (0,0) and (d,0) respectively They start moving with speed VA=Vˆi+Vˆj and VB=−Vˆj If R is magnitude of relative separation between them and T0 be the time when separation between them is minimum, then
View Solution

