Two particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
q/2m
q/m
2q/m
q/πm
The correct Answer is:a
To solve the problem, we need to find the ratio of the magnitudes of the magnetic moment of the system to its angular momentum about the center of the rod. Let's break it down step by step.
Step 1: Understanding the System
We have two particles, each with mass m and charge q, attached to the ends of a rigid rod of length 2R. The rod is rotating about a perpendicular axis through its center.
Step 2: Calculate the Magnetic Moment
The magnetic moment M of a system can be calculated using the formula:
M=I⋅A
where I is the current and A is the area swept by the charges.
1. Calculate the Current I:
The total charge Q that is effectively moving is 2q (since there are two charges). The time period T for one complete rotation is given by:
T=2πω
Therefore, the current I is:
I=Total chargeTime period=2qT=2q⋅ω2π=qωπ
2. Calculate the Area A:
The area swept by the charges as they rotate is a circle with radius R:
A=πR2
3. Calculate the Magnetic Moment M:
Substituting I and A into the magnetic moment formula:
M=I⋅A=(qωπ)⋅(πR2)=qωR2
Step 3: Calculate the Angular Momentum
The angular momentum L of the system can be calculated using the formula:
L=I⋅ω
where I is the moment of inertia of the system.
1. Calculate the Moment of Inertia I:
The moment of inertia I for two point masses at a distance R from the center is:
I=mR2+mR2=2mR2
2. Calculate the Angular Momentum L:
Now substituting I into the angular momentum formula:
L=(2mR2)⋅ω
Step 4: Calculate the Ratio of Magnetic Moment to Angular Momentum
Now, we can find the ratio ML:
ML=qωR22mR2ω
Cancelling ω and R2 from the numerator and denominator, we get:
ML=q2m
Final Answer
Thus, the ratio of the magnitudes of the magnetic moment of the system to its angular momentum about the center of the rod is:
ML=q2m
---
We have two particles, each with mass m and charge q, attached to the ends of a rigid rod of length 2R. The rod is rotating about a perpendicular axis through its center.
The magnetic moment M of a system can be calculated using the formula:
M=I⋅A
where I is the current and A is the area swept by the charges.
The total charge Q that is effectively moving is 2q (since there are two charges). The time period T for one complete rotation is given by:
T=2πω
Therefore, the current I is:
I=Total chargeTime period=2qT=2q⋅ω2π=qωπ
The area swept by the charges as they rotate is a circle with radius R:
A=πR2
Substituting I and A into the magnetic moment formula:
M=I⋅A=(qωπ)⋅(πR2)=qωR2
The angular momentum L of the system can be calculated using the formula:
L=I⋅ω
where I is the moment of inertia of the system.
The moment of inertia I for two point masses at a distance R from the center is:
I=mR2+mR2=2mR2
Now substituting I into the angular momentum formula:
L=(2mR2)⋅ω
Now, we can find the ratio ML:
ML=qωR22mR2ω
Cancelling ω and R2 from the numerator and denominator, we get:
ML=q2m
Thus, the ratio of the magnitudes of the magnetic moment of the system to its angular momentum about the center of the rod is:
ML=q2m
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Multiple Correct
9 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Comprehension
2 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives True /false
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
Two balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
Knowledge Check
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML2/4BML2/2CML2D2ML2Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
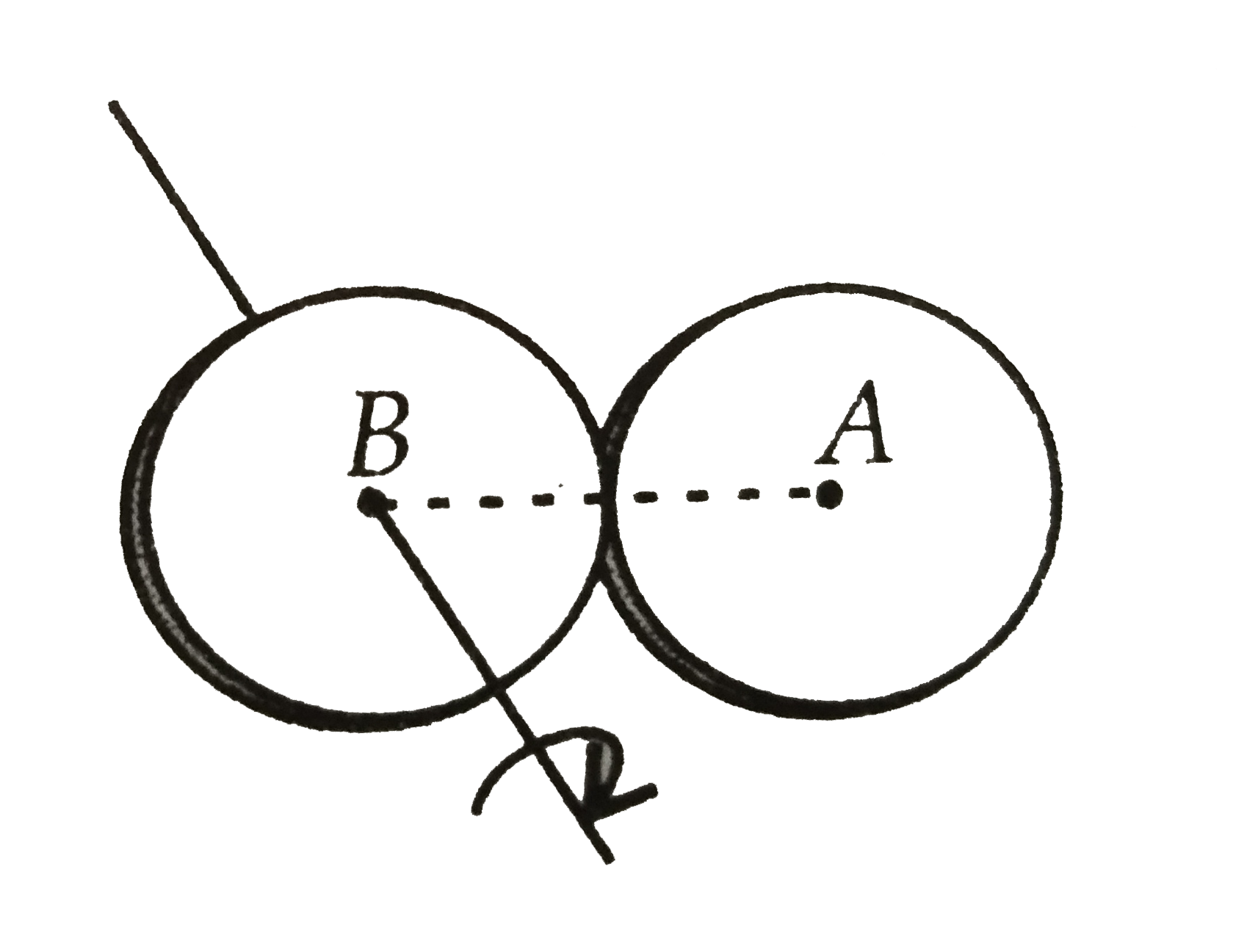 A2Mr2B3Mr2C4Mr2D5Mr2
A2Mr2B3Mr2C4Mr2D5Mr2
The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionTwo particles of masses m1andm2 are joined by a light rigid rod of length r. The system rotates at an angular speed ω about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is L=μr2ω where μ is the reduced mass of the system defined as μ=m1m2m1+m2
View SolutionTwo small balls A and B each of mass m, are attached tightly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed ω. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View Solution
