Two particles have equal mass m and electric charge of equal magnitude (q) and opposite sign. The particles are held at rest at co-ordinates (– a, 0) and (a, 0) as shown in the figure. The particles are released simultaneously. Consider only the electrostatic force between the particles and the force applied by the external magnetic field on them.
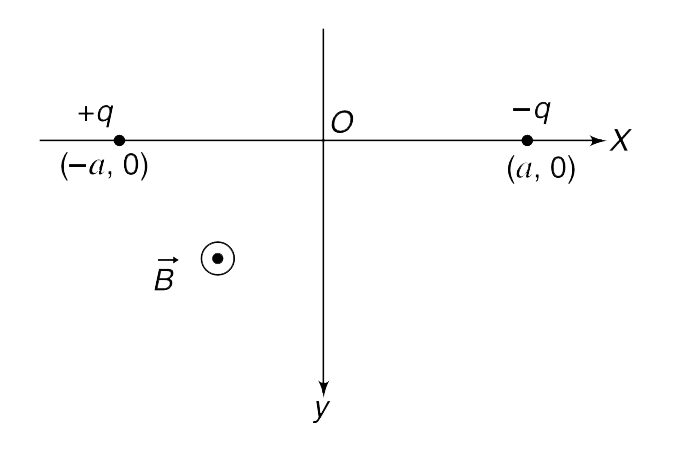
Two particles have equal mass m and electric charge of equal magnitude (q) and opposite sign. The particles are held at rest at co-ordinates (– a, 0) and (a, 0) as shown in the figure. The particles are released simultaneously. Consider only the electrostatic force between the particles and the force applied by the external magnetic field on them. (a) Find the speed of negatively charged particle as function of its x co-ordinate. (b) Find the y component of velocity of the negative particle as a function of its x co-ordinate.
(a) Find the speed of negatively charged particle as function of its x co-ordinate.
(b) Find the y component of velocity of the negative particle as a function of its x co-ordinate.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:(a)V=√kq22m(1x−1a) (b)Vy=qBm(a−x)

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for Two particles have equal mass m and electric charge of equal magnitude (q) and opposite sign. The particles are held at rest at co-ordinates (– a, 0) and (a, 0) as shown in the figure. The particles are released simultaneously. Consider only the electrostatic force between the particles and the force applied by the external magnetic field on them. (a) Find the speed of negatively charged particle as function of its x co-ordinate. (b) Find the y component of velocity of the negative particle as a function of its x co-ordinate. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12PHYSICSMOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Three charged particle sare in equilibrium under their electrostatic forces only. Then

    Athe particle smust be collinear
    Ball the charges cannot have the same magnitude
    Call the charges cannot have the same sign
    Dthe equilibrium is unstable

  • A charged particle is moved along a magnetic field line. The magnetic force on the particle is

    Aalong its velocity
    Bopposite to its velocity
    Cperpendicular to its velocity
    Dzero

  • A charged particle is moving along a magnetic field line. The magnetic force on the particle is

    Aalong its velocity
    Bopposite to its velocity
    Cperpendicular to its velocity
    Dzero