Two particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance 'a' from the center P (as shown in figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is :Solution in Kannada
F2ma√a2−x2
F2ma√x−x2
F2mxa
F2m√a2−x2x
The correct Answer is:b
As shown in fig. (i) the separation between the twomasses is 2x. Each mass will move in the horizontal direction towards each other as the force .F. acts vertically. Let the tension in each part of the string be T. The state of forces at the point P and on the mass A are shown in fig. (ii) and (ii) above. When the separation x is reached net force at the point P is given by:

Fig. (ii) 2T sin theta=F…(i)
Also for the mass A, Fig. ..(ii)
R+Tsinθ=mg...(ii)
Tcosθ=mf...(iii)
where .f is the acceleration with which each ball moves. From (1) and (iii)
Acceleration, f=Fcosθ2m=F2m×x√a2x2
Hence (b) is the correct choice
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - MULTIPLE CHOICE QUESTION (LEVEL-III)
2 Videos
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - RECENT COMPETITIVE QUESTIONS
7 Videos
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Revision test
43 Videos
- HEAT AND THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - Recent Competitve Questions
17 Videos
- MAGNETOSTATICSBOOK - MODERN PUBLICATIONCHAPTER - MAGNETOSTATICSEXERCISE - RECENT COMPETITIVE QUESTION
5 Videos
Similar Questions
A block of mass m is placed on a surface with a vertical cross section given by y=x36If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is :
View SolutionA ball rests upon a flat piece of paper on a table top.The paper is pulled horizontally but quickly towards right as shown. Relative to its initial position with respect to the table, the ball :
(A) remains stationary if there is no friction between the paper and the ball.
(B) moves to the left and starts rolling backwards, i.e.to the left if there is a friction between the paper and the ball
(C) moves forward, i.e. in the direction in which the paper is pulled Here, the correct statement/s is/are :
View SolutionWhen a carpet is beaten with a stick, dust comes out of it. Explain.
View SolutionThe temperature of a gas contained in a closed vessel of constant volume increases by 1∘C when the pressure of the gas is increased by 1%. The initial temperature of the gas is:
View SolutionA gyromagnetic ratio of the electron revolving in a circular orbit of hydrogen atom is 8.8×1010Ckg−1. What is the mass of the electron? Given charge of the electron =1.6×10−19C.
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
View SolutionA block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q = 1muC , mass of each particle m=6g . The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface. What is the tension in the string?
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q = 1muC , mass of each particle m=6g . The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface. What is the tension in the string when velocity is maximum.
View SolutionTwo particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
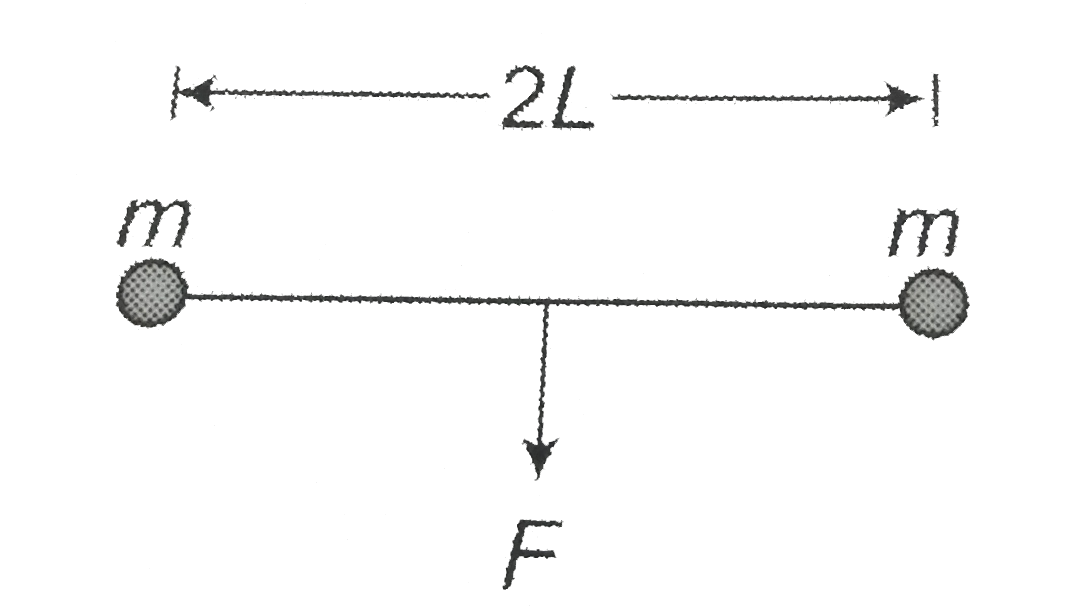
View SolutionA cylinder C rests on a horizontal surface. A small particle of mass m is held in equilibrium connected to an overhanging string as shown. The other end of the mass less string is being pulled horizontally by a force F as shown. Find F.
View SolutionTwo block of mass 5 kg and 10 kg respectively are connected by a massless string as shown in the figure. The whole system is kept on a frictionless surface. A force of 50 N is applied horizontally as shown in the figure. The tension T in the string will be
View SolutionTwo masses M and m are connected by a weightless string. They are pulled by a force F on a frictionless horizontal surface. The tension in the string will be
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a . The whole system is kept on a frictionless horizontal surface with the string held tight so that, each mass is at a distance 'a' from the center P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x , is :
View SolutionTwo particles of mass 'm' each are tied at eh ends of a light string of length '2a' The whole system is kept on frictionless horizontal surface with the string held tight so that each mass is at a distance 'a' from the centre P (as shown in figure). Now the mid point of the string is pulled vertically upwards with a small but constant force F As a result, the particles move towards each other on the surface the magnitude of acceleration, when the separation between them becomes 2x is:
View Solution
