Question

A block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.

Explanation

Let the force applied by string to the block be T. For part (a), consider one system is block and other string. Let the acceleration of the system (block +string) be a.

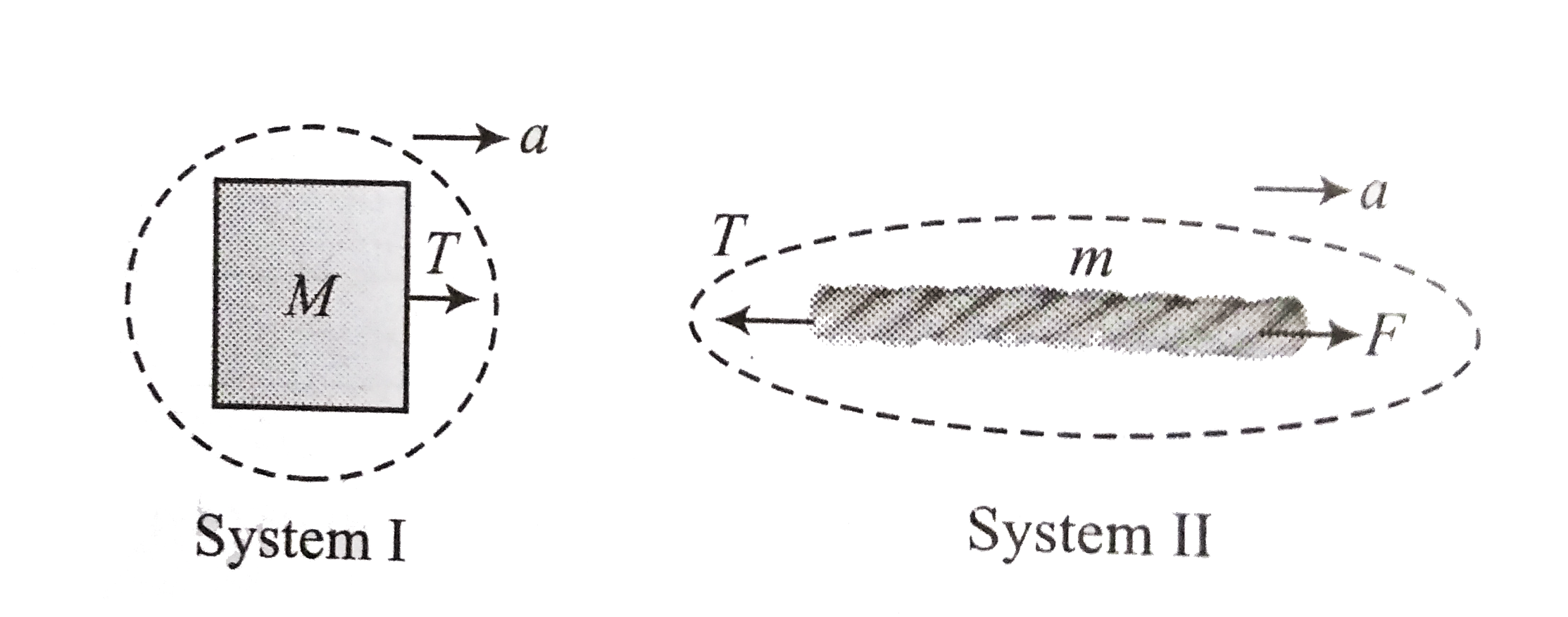
Now we apply Newton's law to each of them.
For system II: F-T=ma ...(i)
For system I:T=ma...(ii)
After solving (i) and (ii), `a=(F)/(M+m), T=(MF)/(M+m)`
(b) Now we have to redefine our system. Choose system 1 as block and half string and system 2 as the other half string . On applying Newton's second law to system 1 and system 2, we have

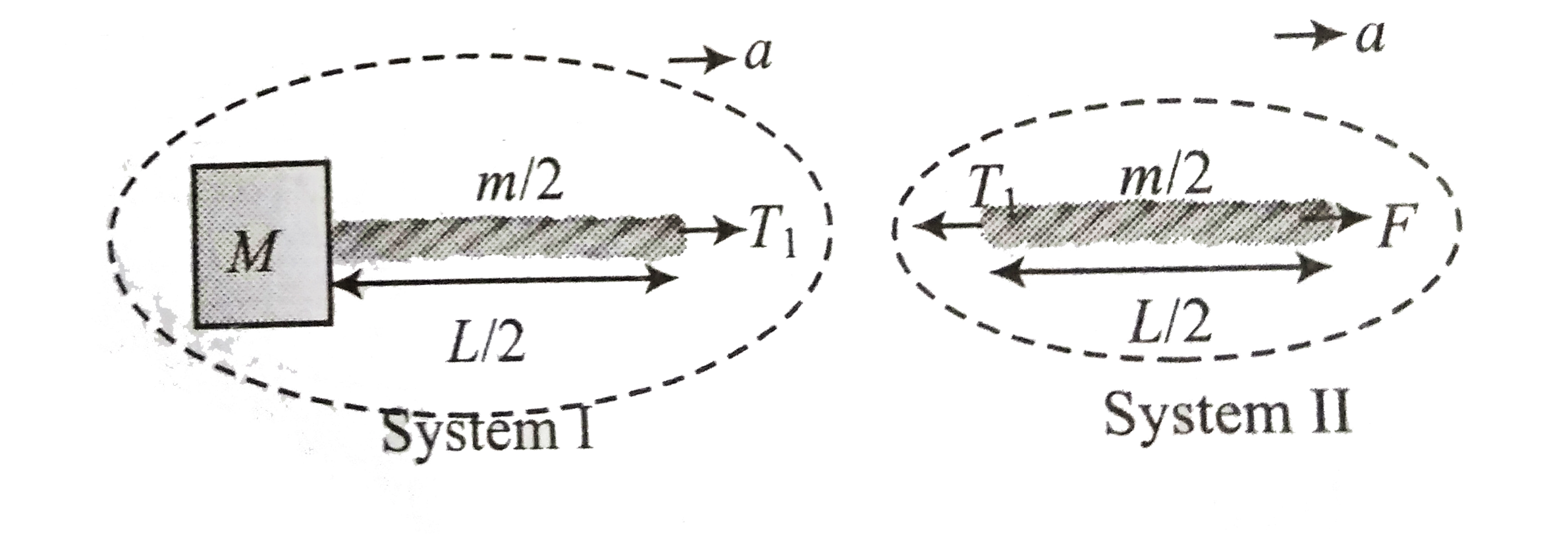
System II: `F=(T_1) = m/2 xx a` ...(iii)
Mass per unit length of string `=m//L`
Hence, mass of `L//2` length of string `m/L xx L/2 = m/2`
System I: `T_(1)=(M+m/2)a`...(iv)
After solivng (iii) and (iv) we get,
`a=(F)/(M+m), T_(1)=((M+m//2)F)/((M+m))`
c. Now we can redefine our system in the block and string of length L-x(system I) and string of length x (system II)

System II: `F-T_(2)=((m)/(L) xx x)a` ...(v)
System I: `T_(2)={m/L (L-x)+M}a` ...(vi)
Solving (v) and (vi) we get
`a=(F)/(M+m) and (T_2) =({m(L-x)//L+M}F)/(M+m)`
Here we see that acceleration in each part is same, but tension changes along the string.