Two particles of masses 2kg and 4kg are approaching towards each other with ccelerations 1m/s2 and 2m/s2, respectively, on a smooth horizontal suface. Then find the acceleration of centre of mass of the system and direction of acceleration of CM.
To find the acceleration of the center of mass (CM) of the system consisting of two particles with masses m1=2kg and m2=4kg, and their respective accelerations a1=1m/s2 and a2=2m/s2, we can follow these steps:
Step 1: Identify the masses and their accelerations
- Mass of particle 1, m1=2kg with acceleration a1=1m/s2
- Mass of particle 2, m2=4kg with acceleration a2=2m/s2
Step 2: Assign directions to the accelerations
- Let's assume the direction of the acceleration of the 2kg mass (particle 1) is positive. Therefore, the acceleration of the 4kg mass (particle 2) moving towards it will be considered negative.
Step 3: Write the equation for the acceleration of the center of mass
The formula for the acceleration of the center of mass aCM is given by:
aCM=m1a1+m2a2m1+m2
Step 4: Substitute the values into the equation
Substituting the values we have:
aCM=(2kg⋅1m/s2)+(4kg⋅(−2m/s2))2kg+4kg
Step 5: Calculate the numerator and denominator
Calculating the numerator:
=2⋅1+4⋅(−2)=2−8=−6
Calculating the denominator:
=2+4=6
Step 6: Compute the acceleration of the center of mass
Now substituting back into the equation:
aCM=−66=−1m/s2
Step 7: Determine the direction of the acceleration of the center of mass
Since aCM is negative, this indicates that the acceleration of the center of mass is in the direction of the 4kg mass (the negative direction we assigned).
Final Answer
The acceleration of the center of mass of the system is −1m/s2, and it is directed towards the 4kg mass.
---
- Mass of particle 1, m1=2kg with acceleration a1=1m/s2
- Mass of particle 2, m2=4kg with acceleration a2=2m/s2
- Let's assume the direction of the acceleration of the 2kg mass (particle 1) is positive. Therefore, the acceleration of the 4kg mass (particle 2) moving towards it will be considered negative.
The formula for the acceleration of the center of mass aCM is given by:
aCM=m1a1+m2a2m1+m2
Substituting the values we have:
aCM=(2kg⋅1m/s2)+(4kg⋅(−2m/s2))2kg+4kg
Calculating the numerator:
=2⋅1+4⋅(−2)=2−8=−6
Calculating the denominator:
=2+4=6
Now substituting back into the equation:
aCM=−66=−1m/s2
Since aCM is negative, this indicates that the acceleration of the center of mass is in the direction of the 4kg mass (the negative direction we assigned).
The acceleration of the center of mass of the system is −1m/s2, and it is directed towards the 4kg mass.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two particles of masses 2 kg and 4 kg are approaching each other with acceleration 1ms−2 and 2ms−2, respectively, on a smooth horizontal surface. Find the acceleration of center of mass of the system.
View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionTwo bodies of masses 4kg and 2kg are moving towards each other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo balls of masses 2kg and 4kg are moved towards each other with velocities 4m/s and 2m/s, respectively, on a frictionless surface. After colliding, the 2kg ball returns back with velocity 2m/s. then find
a. velocity of the 4kg after collision
b. coefficient of restitution e,
c. impulse of deformation JD
d. maximum potential energy of deformation,
e. impulse of reformation JR
View SolutionTwo particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then

View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionTwo particles of masses m1=6kg&m2=4kg move towards each other with u1=3m/sec&u2=6m/sec respectively. If they collide elastically, find the impulse of the particles.
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
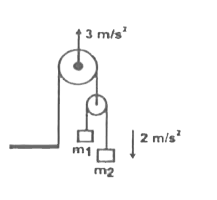
View Solution
