Two particles of masses m1=6kg&m2=4kg move towards each other with u1=3m/sec&u2=6m/sec respectively. If they collide elastically, find the impulse of the particles.
The correct Answer is:36 N-s
To solve the problem step by step, we will follow the principles of conservation of momentum and the coefficient of restitution for elastic collisions.
1. Identify the Given Values:
- Mass of particle 1, m1=6kg
- Mass of particle 2, m2=4kg
- Initial velocity of particle 1, u1=3m/s (to the right)
- Initial velocity of particle 2, u2=−6m/s (to the left, hence negative)
2. Use Conservation of Momentum:
The total momentum before the collision must equal the total momentum after the collision. Therefore, we can write:
m1u1+m2u2=m1v1+m2v2
Substituting the known values:
6×3+4×(−6)=6v1+4v2
Simplifying this gives:
18−24=6v1+4v2
−6=6v1+4v2(Equation 1)
3. Use the Coefficient of Restitution:
For an elastic collision, the coefficient of restitution e=1. The formula for the coefficient of restitution is:
e=Relative velocity after collisionRelative velocity before collision
Thus,
1=v2−v1u1−u2
Substituting the values:
1=v2−v13−(−6)
1=v2−v19
Therefore,
v2−v1=9(Equation 2)
4. Solve the System of Equations:
We now have two equations:
- Equation 1: 6v1+4v2=−6
- Equation 2: v2−v1=9
From Equation 2, we can express v2 in terms of v1:
v2=v1+9
Substitute v2 into Equation 1:
6v1+4(v1+9)=−6
Simplifying this:
6v1+4v1+36=−6
10v1+36=−6
10v1=−42
v1=−4.2m/s
Now substituting v1 back to find v2:
v2=−4.2+9=4.8m/s
5. Calculate the Impulse:
The impulse J experienced by each particle can be calculated using the impulse-momentum theorem:
J=Δp=m(v−u)
For particle 1:
J1=m1(v1−u1)=6(−4.2−3)=6(−7.2)=−43.2Ns
The magnitude of the impulse is:
|J1|=43.2Ns
For particle 2:
J2=m2(v2−u2)=4(4.8−(−6))=4(4.8+6)=4(10.8)=43.2Ns
Final Answer:
The impulse of both particles is 43.2Ns.
- Mass of particle 1, m1=6kg
- Mass of particle 2, m2=4kg
- Initial velocity of particle 1, u1=3m/s (to the right)
- Initial velocity of particle 2, u2=−6m/s (to the left, hence negative)
The total momentum before the collision must equal the total momentum after the collision. Therefore, we can write:
m1u1+m2u2=m1v1+m2v2
Substituting the known values:
6×3+4×(−6)=6v1+4v2
Simplifying this gives:
18−24=6v1+4v2
−6=6v1+4v2(Equation 1)
For an elastic collision, the coefficient of restitution e=1. The formula for the coefficient of restitution is:
e=Relative velocity after collisionRelative velocity before collision
Thus,
1=v2−v1u1−u2
Substituting the values:
1=v2−v13−(−6)
1=v2−v19
Therefore,
v2−v1=9(Equation 2)
We now have two equations:
- Equation 1: 6v1+4v2=−6
- Equation 2: v2−v1=9
v2=v1+9
Substitute v2 into Equation 1:
6v1+4(v1+9)=−6
Simplifying this:
6v1+4v1+36=−6
10v1+36=−6
10v1=−42
v1=−4.2m/s
v2=−4.2+9=4.8m/s
The impulse J experienced by each particle can be calculated using the impulse-momentum theorem:
J=Δp=m(v−u)
For particle 1:
J1=m1(v1−u1)=6(−4.2−3)=6(−7.2)=−43.2Ns
The magnitude of the impulse is:
|J1|=43.2Ns
J2=m2(v2−u2)=4(4.8−(−6))=4(4.8+6)=4(10.8)=43.2Ns
The impulse of both particles is 43.2Ns.
Similar Questions
Find the loss of KE of the two particles of mass m1=3kg&m2=6kg, moving towards each other with speed u1=5m/s,u2=10m/s respectively. The coefficient of restitution of collision of the particles is e = 0.5.
View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionTwo particles of masses 2kg and 4kg are approaching towards each other with ccelerations 1m/s2 and 2m/s2, respectively, on a smooth horizontal suface. Then find the acceleration of centre of mass of the system and direction of acceleration of CM.
View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionTwo balls of masses 2kg and 4kg are moved towards each other with velocities 4m/s and 2m/s, respectively, on a frictionless surface. After colliding, the 2kg ball returns back with velocity 2m/s. then find
a. velocity of the 4kg after collision
b. coefficient of restitution e,
c. impulse of deformation JD
d. maximum potential energy of deformation,
e. impulse of reformation JR
View SolutionTwo particles of mass m & 2m have velocities uˆj & uˆi respectively . They collide completely inelastically. Find the loss in kinetic energy of the system.
View SolutionTwo particles of mass m & 2m have velocities uˆj & uˆi respectively . They collide completely inelastically. Find the loss in kinetic energy of the system.
View SolutionTwo particles of masses m1 and m2 and velocities u1 and αu1(α≠0) make an elastic head on collision. If the initial kinetic energies of the two particles are equal and m1 comes to rest after collision, then
View SolutionTwo men to masses 80kg and 60kg are standing on a wood plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving towards each other with speeds 1m/s and 2m/s respectively then find the velocity of the plank by which it starts moving.
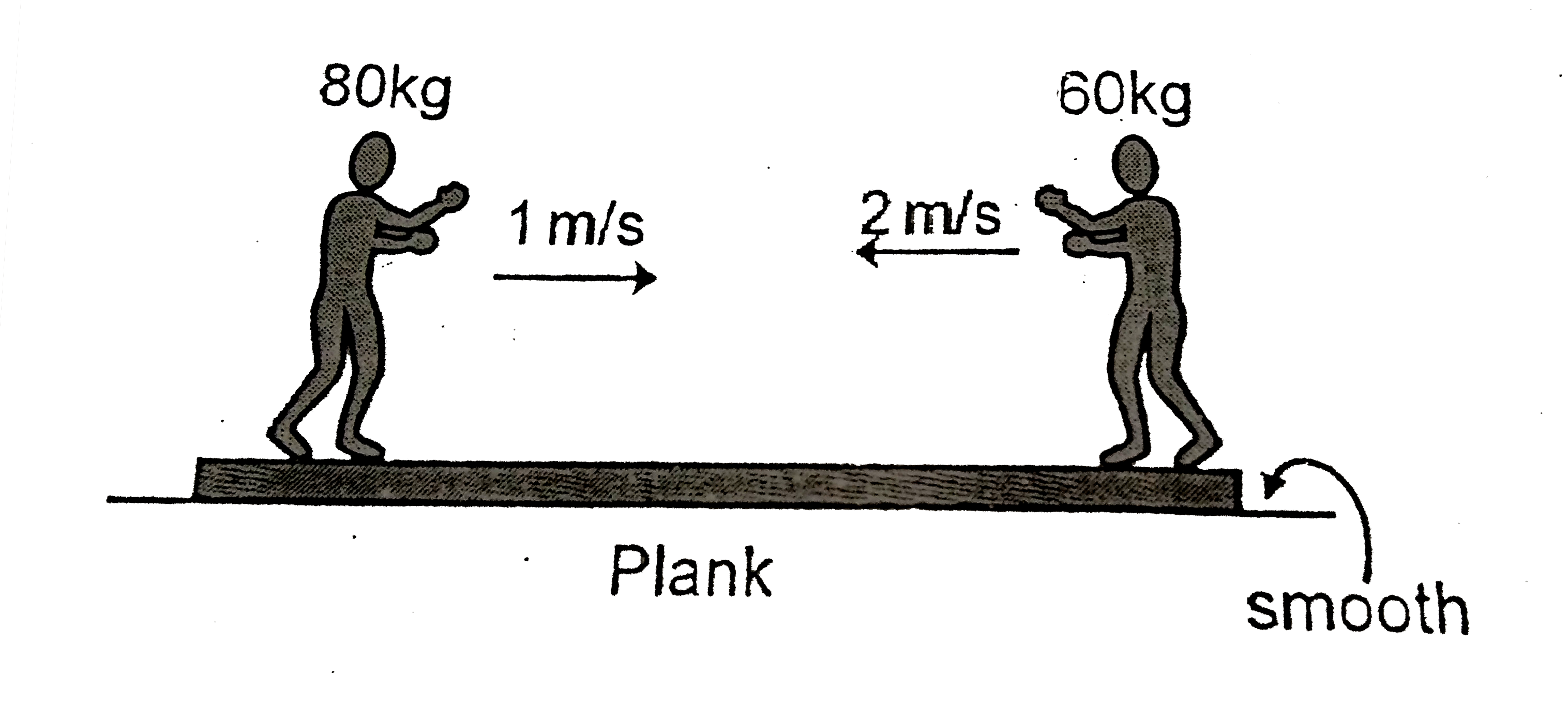
View SolutionTwo particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
View Solution
