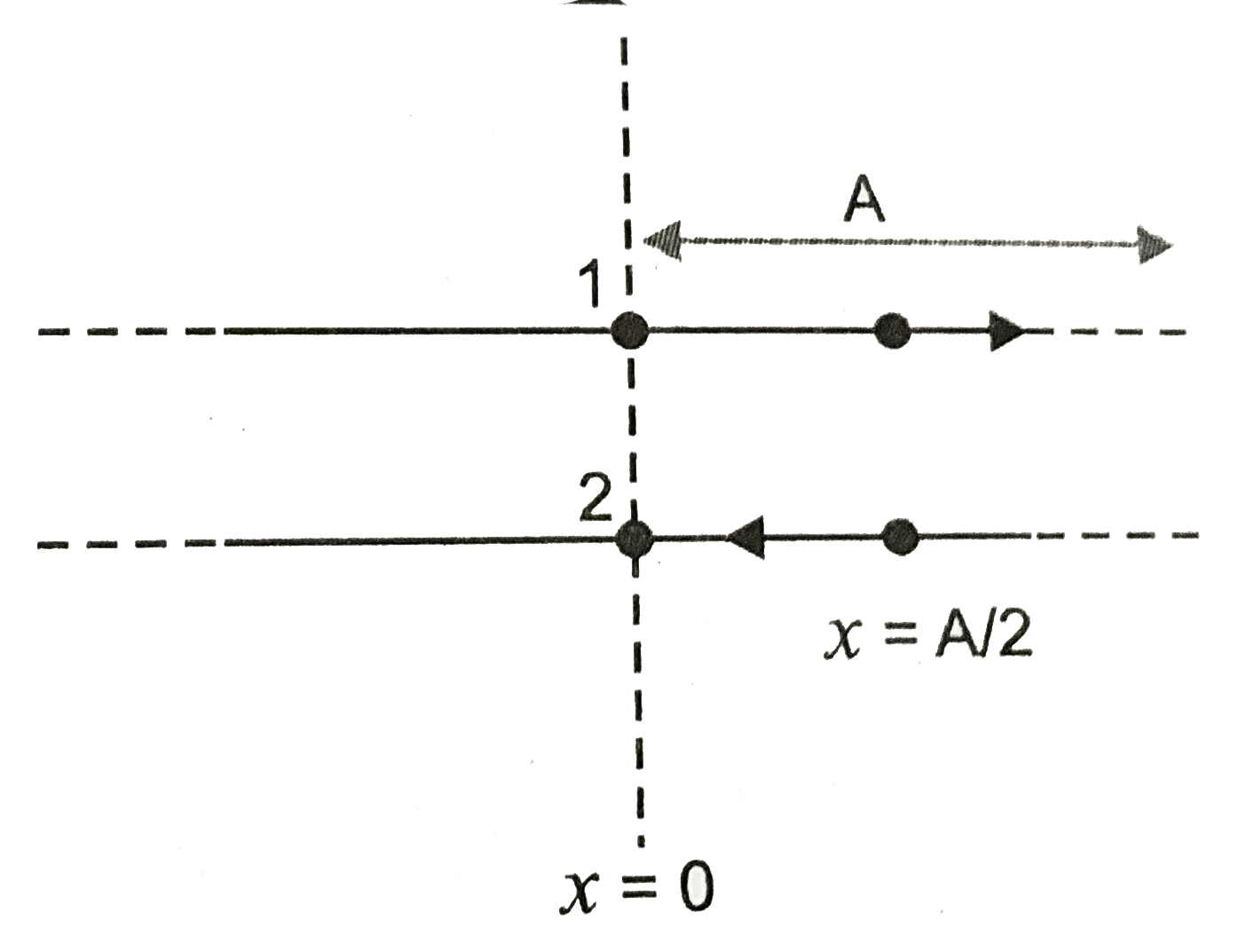
Two pearticle are oscillation along two close parallel straght lines side by side with the same frequency and amplitude They pass each other moving in opposite directions when their displacement is half of the on a stright line perpendicular to the part of the two particle The phase difference is

$2 π / 3$

$π$

$π / 6$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The phase difference is:-
A $\frac{π}{6}$
B0
C $\frac{2 π}{3}$
D $π$
Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The phase difference is:-
A $\frac{π}{6}$
B0
C $\frac{2 π}{3}$
D $π$
Two particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
A $\frac{5 π}{6}$
B $\frac{4 π}{3}$
C $\frac{π}{6}$
D $\frac{2 π}{3}$