Two pendulums each of length are initially situated as shown in Fig. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?

The correct Answer is:A
Applying the law of conservatioin of momentum
…………i
where is the velocity with which collides with therefore
Now, let the centre of mass rise through a height after collision. In this case, the kinetic enerty of system is converted into potential energy at maximum height
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two balls having masses m and 2m are fastened to two light strings of same length l figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. a. Find velocities of the balls just after their collision. b. How high will the balls rise after the collision.

View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View Solution
Knowledge Check
Two pendulum each of length l are initial situated as shown in figure. The first pendulum is released and strikes the second . Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the center of mass rise after the collision?
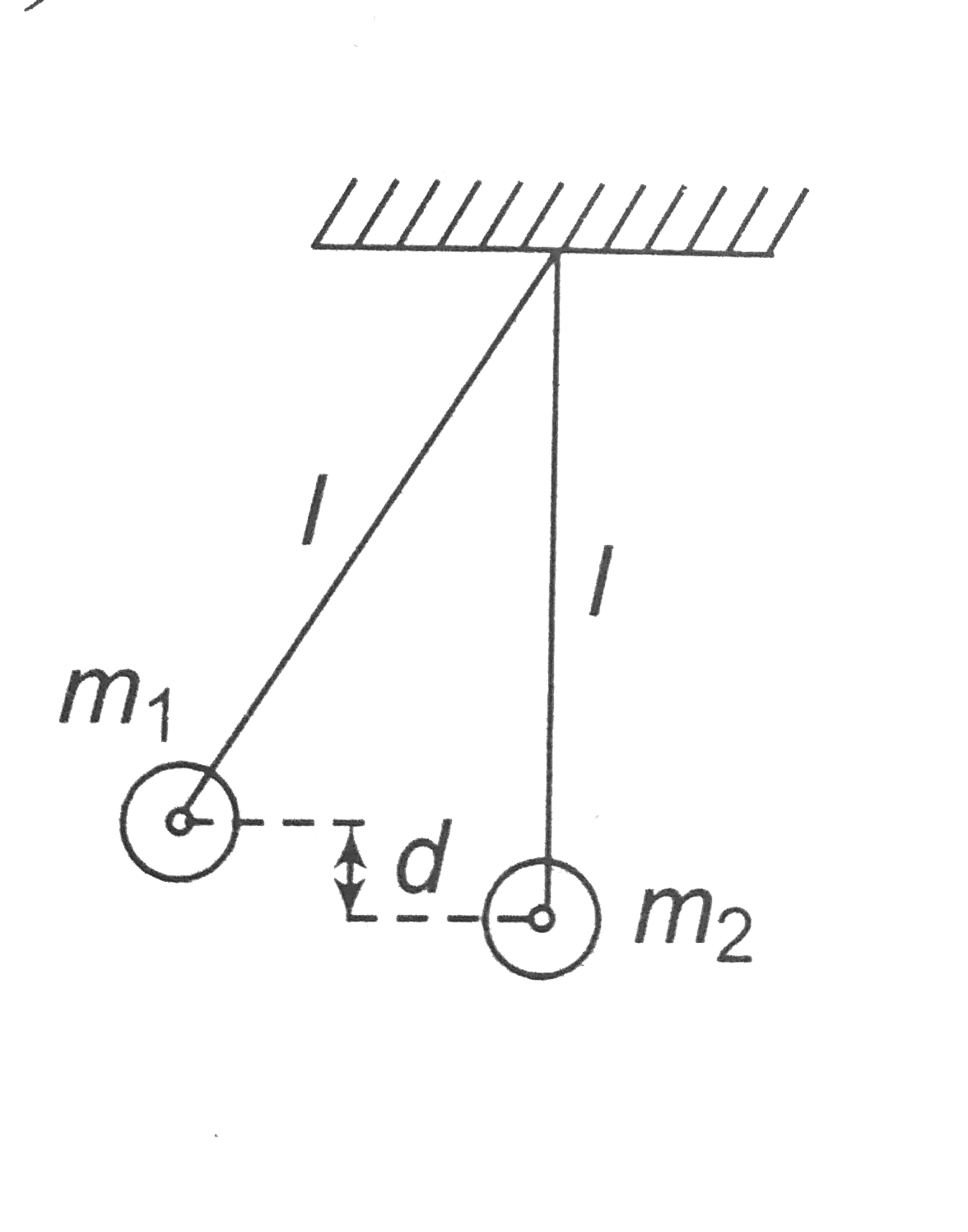 Ad[m1(m1+m2)]2Bd[m1(m1+m2)]Cd(m1+m2)2m2Dd[m2(m1+m2)]2
Ad[m1(m1+m2)]2Bd[m1(m1+m2)]Cd(m1+m2)2m2Dd[m2(m1+m2)]2Two pendulums each of lengh l are initially situated as shown in figure. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and frictional effects. How high does the centre of mass rise after the collision ?
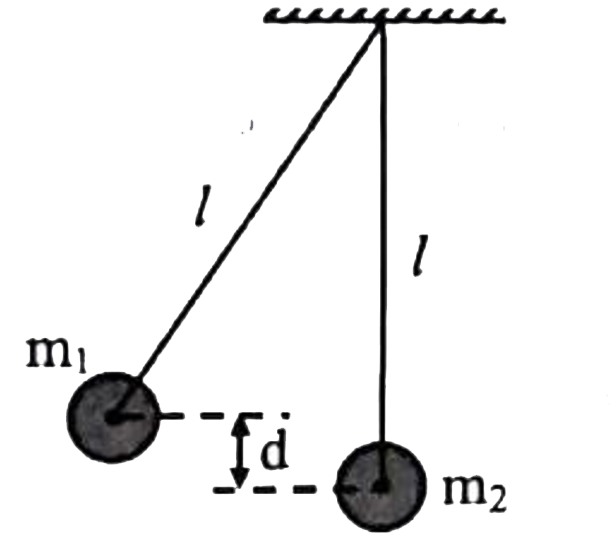 Ad[m1(m1+m2)]2Bd[m1(m1+m2)]Cd(m1+m2)2m2Dd[m2(m1+m2)]2
Ad[m1(m1+m2)]2Bd[m1(m1+m2)]Cd(m1+m2)2m2Dd[m2(m1+m2)]2A ball of mass m moving horizontally at a speed v collides with the bob of a simple pendulum at rest. The mass of the bob is also m. If the collision is perfectly inelastic and both balls sticks, the height to which the two balls rise after the collision will be given by:
Av2gBv22gCv24gDv28g
Two massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View Solution
