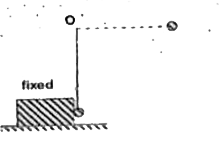
Two balls having masses m and 2m are fastened to two light strings of same length l figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. a. Find velocities of the balls just after their collision. b. How high will the balls rise after the collision.

Video Solution

Text Solution

Verified by Experts

Let the velocilty of m reaching at lower end
$= v_{1}$
From work energy principle
$∴ (\frac{1}{2}) \times m v_{1}^{2} - (\frac{1}{2}) \times m {(0)}^{2} = m g l$
$\to v_{1} = \sqrt{2 g l}$
similarly velocity of heavy block will be ltbr> $v_{2} = s q t (2 g l)$
$∴ V_{1} = v_{2} = u (s a y)$
Let fiN/A,l velocity of m and 2m are $v_{1} and v_{2}$ respectively.
According to law of conservation of momenum
$\to m \times u - 2 μ = m v_{1} + 2 m v_{2}$
$\to v_{1} + 2 v_{2} = - u$
$A g a \in v_{1} - v - 2 = [(u - v)] = - 2 u$
Substracting
$3 v_{2} = u$
$\to v_{2} = \frac{u}{3} = \frac{\sqrt{2 g l}}{3}$
substituting in ii ltbr> $v_{1} - v_{2} = - 2 u$
$\to v_{1} = - 2 u + v_{2}$
$= - 2 u + (\frac{u}{3})$
$= \frac{- 5}{3} u = \frac{- 5}{3} \times \sqrt{2 g l}$
$\frac{\sqrt{50 g l}}{3}$
b. putting the work energy principle
(1/2)xx2mxx(0)^2-(1/2)xx2mxx(v_2)^2 $< b r >$ =-2mxxgxxh $< b r >$ [hrarr $h e i g h t r e a c h e d b y h e a v y b a l l]$
$\to h = (\frac{L}{9})$
similarly
$(\frac{1}{2}) \times m x {(0)}^{2} - (\frac{1}{2}) \times m v_{1}^{2} = m \times g \times h_{2}$
[height reached by small ball] ltbr> $(\frac{1}{2}) \times \frac{50 g L}{9} g \times h_{2}$
$h_{2} = \frac{0.25 L}{9}$
some $h_{2}$ is more than 2L the velocity at highest point will not be zero.

Updated on:21/07/2023