Two perfectly smooth elastic discs A and B, one k times as massive as the other, rest on a smooth horizontal table. The disc A is made to move towards B with velocity u and make a head on collision. Calculate the fraction of the kinetic energy transferred to B from A. Also show that the value of this fraction is the same whether B is k times as massive as A or vice versa.
The correct Answer is:[4k(k+1)2]
Step by step video, text & image solution for Two perfectly smooth elastic discs A and B, one k times as massive as the other, rest on a smooth horizontal table. The disc A is made to move towards B with velocity u and make a head on collision. Calculate the fraction of the kinetic energy transferred to B from A. Also show that the value of this fraction is the same whether B is k times as massive as A or vice versa. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Advance McQ
20 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
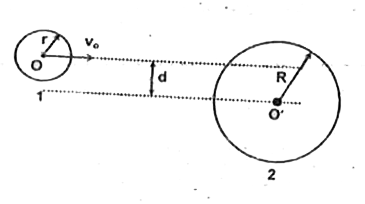
A disc of mass m is moving with constant speed v0 on a smooth horizontal table. Another disc of mass M is placed on the table at rest as shown in the figure. If the collision is elastic, find the velocity of the disc after collision. Both disc lie on the same horizontal plane of the table.
View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View Solution
Knowledge Check
A ball of mass 'm' moving with speed 'u' undergoes a head-on elastic collision with a ball of mass 'nm' initially at rest. Find the fraction of the incident energy transferred to the second ball.
An1+nBn(1+n)2C2n(1+n)2D4n(1+n)2Two balls A & B of mass m1 and m2 are kept on a horizontal smooth surface. A is given a velocity towards B so that they perform head on collision
AIf m1=m2 and collision is elastic. A stops and B moves with the velocity of A after collisionBImpulses on A and B during collision are same in magnitude whether it is elastic or inelastic collisionCImpulses on A and B collision are equal in magnitude only if m1=m2DIf m1>m2, though impulses are same in magnitude velocity of A is still the same direction.A neutron in a nuclear reactor collides head on elastically with the nucleus of a carbon atom initially at rest. The fraction of kinetic energy transferred from the neutron to the carbon atom is
A1112B211C48121D48169
A particle of mass m moving with some velocity on a smooth surface strikes another particle of mass ηm at rest , elasticity head - on. What fraction of incident K.E. is transferred to the particle of mass ηm.
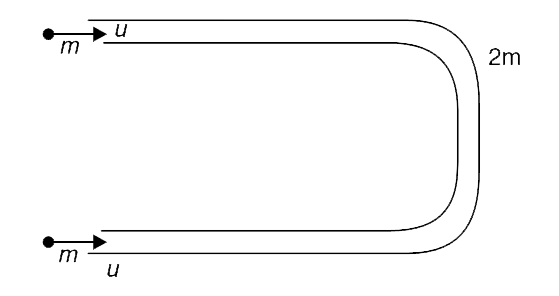
View SolutionA smooth hollow U shaped tube of mass 2m is lying at rest on a smooth horizontal table. Two small balls of mass m, moving with velocity u enter the tube simultaneously in symmetrical fashion. Assume all collisions to be elastic. Find the final velocity of the balls and the tube.
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
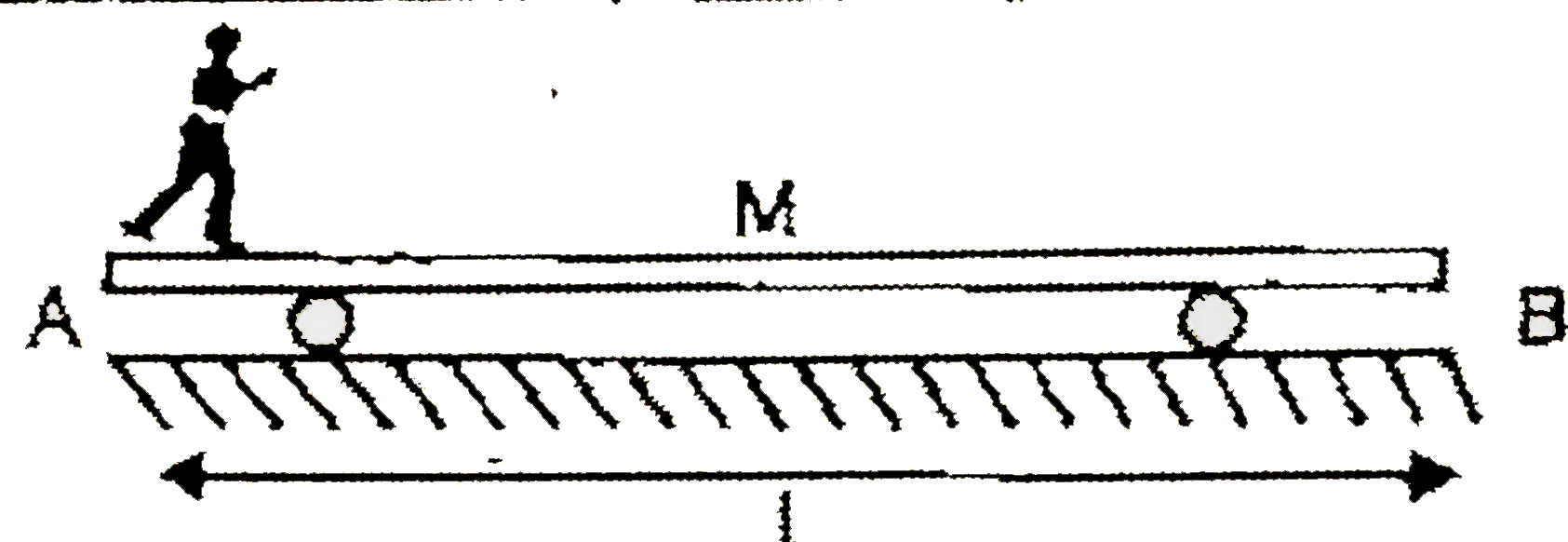
The time taken by the man to reach the other end is:
View SolutionA ball of mass 'm' moving with speed 'u' undergoes a head-on elastic collision with a ball of mass 'nm' initially at rest. Find the fraction of the incident energy transferred to the second ball.
View SolutionConsider the elastic collision f two bodies A and B of equal mass. Initially B is at rest and A moves with velocity v. After the collision -
View Solution
