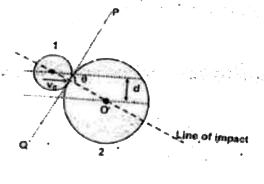
A disc of mass m is moving with constant speed v0 on a smooth horizontal table. Another disc of mass M is placed on the table at rest as shown in the figure. If the collision is elastic, find the velocity of the disc after collision. Both disc lie on the same horizontal plane of the table.

sinθ=dr+R
For mass m :
Momentum before impact
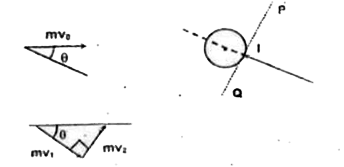
Momentum after impact

For mass M :
Momentum before impact = 0
Momentum after impact
Net impulse on the system = 0
Momentum of the system is conserved.
mv0cosθ+0=mv1+Mv3 ....(i)
mv0sinθ+0=mv2+Mv4 ....(ii)
Individually for mass m and M, the impulse along the tangent = 0
∴ For mass m,mv0sinθ=mv2 ....(iii)
For mass M, 0=Mv4 .... (iv)
As the collision is elastic
e=−v3−v10−v0cosθ=1.
v3−v1=v0cosθ ....(v)
Solving equations (i) through (v)
v2=v0sinθ, v4=0
v3=2mv0cosθm+M,v1=(m−Mm+M)v0cosθ
It can be verified that, 12mv20=12m(v21+v22)+12M(v23+v24)
⇒ The kinetic energy is conserved in an elastic impact.
Special case : If m = M
v1=0,v0sinθ
v3=v0cosθ,v4=0.
Note : The impulse along the common tangent during an impact may not be always negligible. For example, when normal reaction is impulsive and the effect of friction is to tbe considered.
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
10 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE)
18 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
A particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View Solution
Knowledge Check
A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
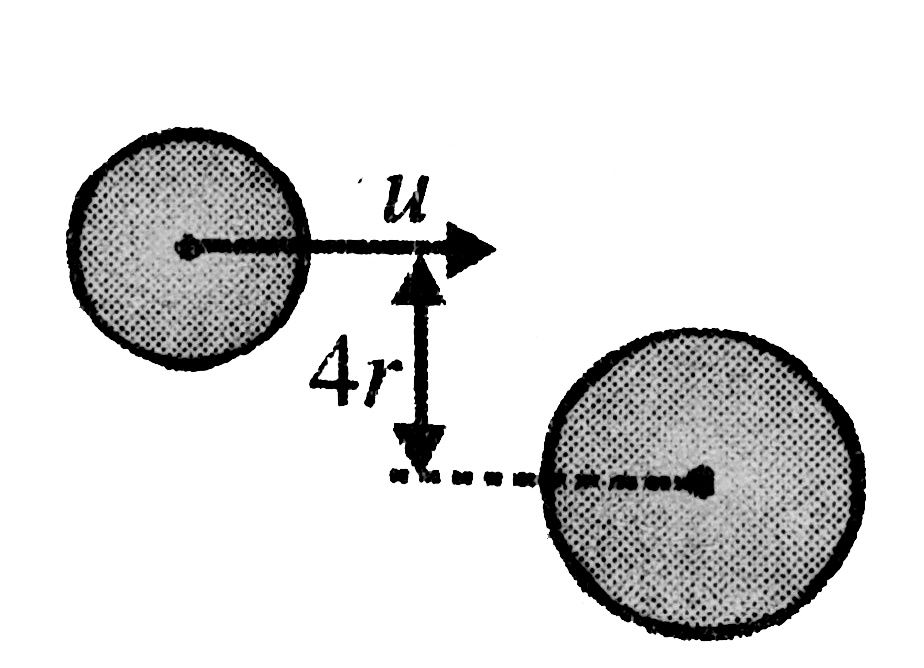 What is the final velocity of the heavier disc?A4v05Bv02C3v05D2v05
What is the final velocity of the heavier disc?A4v05Bv02C3v05D2v05A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 A(2u3R)B(3u3R)C(5u3R)D(2u5R)
A(2u3R)B(3u3R)C(5u3R)D(2u5R)A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
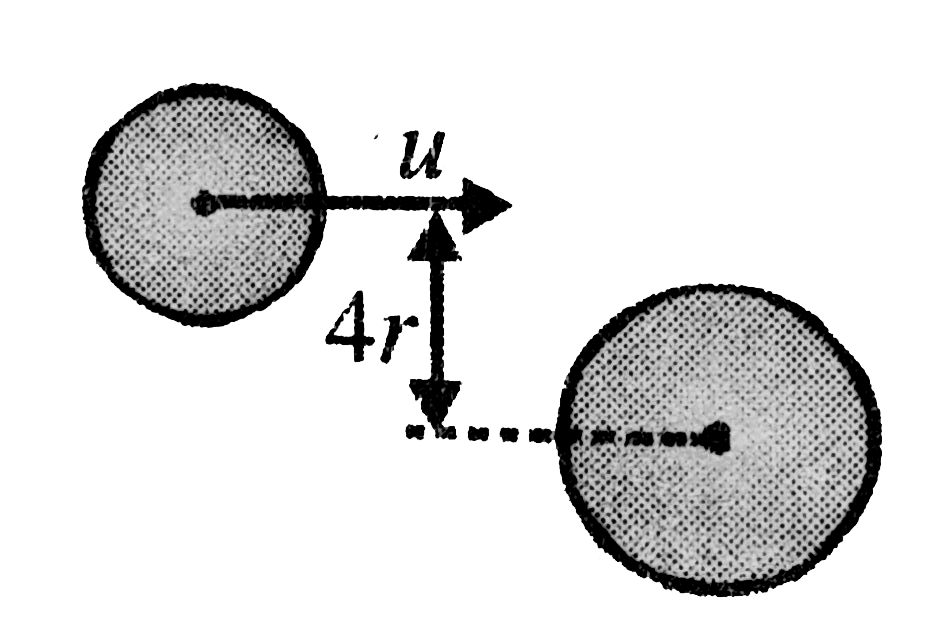
What is the magnitude of normal component of final velocity of the smaller disc'?Au5B2u512C3u5D4u5

A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
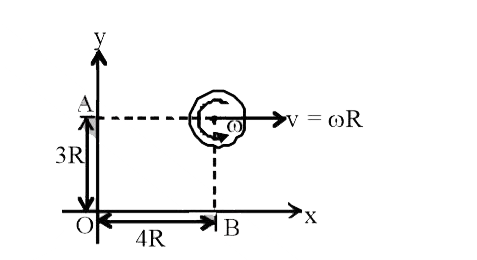
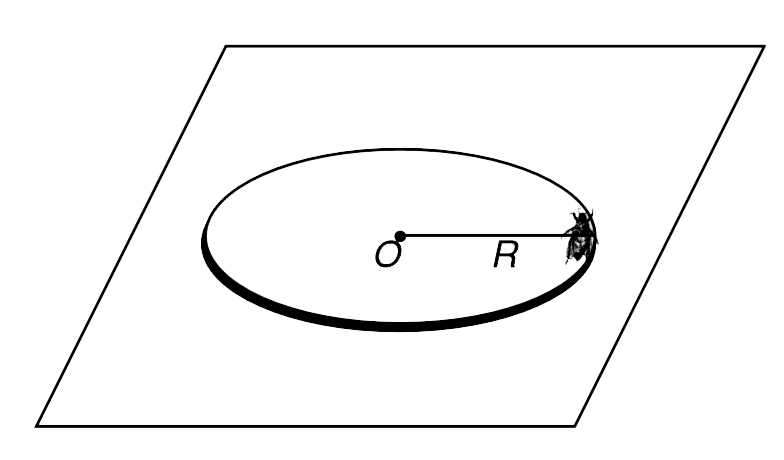
View SolutionA disc of mass M and radius R is kept flat on a smooth horizontal table. An insect of mass m alights on the periphery of the disc and begins to crawl along the edge.
(a) Describe the path of the centre of the disc.
For what value of mM the centre of the disc and the insect will follow the same path ?
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
What is the magnitude of normal component of final velocity of the smaller disc'?
View Solution
