Two point charges of different magnitudes and of opposite signs are separated by some distance. There can be.
only on the point in space where net electric field intensity is zero.
only two points in space where net electric potential is zero
infinite number of points in space where net electric field intensity is 0
infinite number of points in space where net electric potential is zero.
The correct Answer is:a.,d.
To solve the problem regarding the two point charges of different magnitudes and opposite signs, we need to analyze the conditions under which the electric field intensity and electric potential can be zero.
Step 1: Understanding the Setup
We have two point charges, Q1 (positive) and Q2 (negative), with |Q1|>|Q2|. Let's assume:
- Q1=+5μC
- Q2=−2μC
These charges are separated by some distance, say d.
Step 2: Electric Field Intensity
The electric field intensity E due to a point charge is given by the formula:
E=k|Q|r2
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge.
Finding Points Where Electric Field is Zero
1. Between the Charges:
- The electric field from Q1 points away from it, while the field from Q2 points towards it. Since Q1 is larger, the electric field cannot be zero between the two charges.
2. Outside the Charges:
- To the left of Q2 (negative charge), the electric field due to Q2 is directed towards it (to the left), and the electric field due to Q1 is directed away from it (to the right). There can be a point where these fields are equal in magnitude but opposite in direction.
- To the right of Q1 (positive charge), the electric field due to Q1 is directed away from it, and the electric field due to Q2 is directed towards it. However, since Q1 is larger, the electric field will not be zero here.
Thus, there is only one point in space (to the left of Q2) where the net electric field intensity is zero.
Step 3: Electric Potential
The electric potential V due to a point charge is given by:
V=kQr
where r is the distance from the charge.
Finding Points Where Electric Potential is Zero
1. Potential Calculation:
- The potential due to Q1 is positive and increases as we move closer to it.
- The potential due to Q2 is negative and increases (becomes less negative) as we move closer to it.
2. Finding Zero Potential:
- There can be multiple points in space where the positive potential from Q1 can equal the negative potential from Q2.
- For example, if we take a point very far away from both charges, the potentials from both charges will approach zero, but they can also cancel each other out at various distances.
Thus, there are infinite points in space where the net electric potential is zero.
Conclusion
From our analysis:
- There is only one point in space where the net electric field intensity is zero.
- There are infinite points in space where the net electric potential is zero.
We have two point charges, Q1 (positive) and Q2 (negative), with |Q1|>|Q2|. Let's assume:
- Q1=+5μC
- Q2=−2μC
The electric field intensity E due to a point charge is given by the formula:
E=k|Q|r2
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge.
1. Between the Charges:
- The electric field from Q1 points away from it, while the field from Q2 points towards it. Since Q1 is larger, the electric field cannot be zero between the two charges.
- To the left of Q2 (negative charge), the electric field due to Q2 is directed towards it (to the left), and the electric field due to Q1 is directed away from it (to the right). There can be a point where these fields are equal in magnitude but opposite in direction.
- To the right of Q1 (positive charge), the electric field due to Q1 is directed away from it, and the electric field due to Q2 is directed towards it. However, since Q1 is larger, the electric field will not be zero here.
The electric potential V due to a point charge is given by:
V=kQr
where r is the distance from the charge.
1. Potential Calculation:
- The potential due to Q1 is positive and increases as we move closer to it.
- The potential due to Q2 is negative and increases (becomes less negative) as we move closer to it.
- There can be multiple points in space where the positive potential from Q1 can equal the negative potential from Q2.
- For example, if we take a point very far away from both charges, the potentials from both charges will approach zero, but they can also cancel each other out at various distances.
From our analysis:
- There is only one point in space where the net electric field intensity is zero.
- There are infinite points in space where the net electric potential is zero.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Integer
5 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Single Correct
56 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
An electric dipole consists of two charges of equal magnitude and opposite sign separately by a distance 2a. The dipole is along the X-axis and is centred at the origin
(i) Calculate the electric potential at point P
(ii) Calculate V at a point far from the dipole.
View SolutionTwo point charges of same magnitude and opposite sign are fixed at point a and B. A third small point charge is to be balanced at point P by the electrostatic force due to these two charges. The point P :

View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign saperated by a distance 2 a as shown in figure . The dipole is along the x axis and is centered at the origin
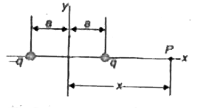
(A) Calculate the electric potential at point P .
(B ) Calculate V at a point far from the dipole .
View SolutionTwo point electric charges of unknown magnitudes and signs are placed a certain distance apart. The electric field intensity is zero at a point not between the charges but on the line joining them. Write two essential conditions for this to happen.
View SolutionThe two quantities are equal in magnitude but opposite in sign
View SolutionTwo point charges Q and -Q/4 are separated by a distance x.
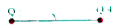
View SolutionTwo fixed point charges +4e and +e units are separated by a distance a. Where should a third point charge be placed for it to be in equilibrium?
View SolutionTwo positive point charges of magnitude Q each are separated by a distance "2a". A test charge 'g0' is located in a plane which is normal to the line joining these charges and midway between them. The locus of the points in this plane for which the force on the test charge has a maximum value is
View SolutionTwo unlike charges of magnitude q are separated by a distance 2d. The potential at a point midway between them is
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View Solution
