Two long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
zero
μ0IπR
2μIπR
μ0I4πR
The correct Answer is:C
To find the magnetic induction at a point midway between two long straight wires carrying currents in opposite directions, we can follow these steps:
Step 1: Understand the Setup
We have two long straight wires, Wire 1 and Wire 2, each carrying a current I in opposite directions. The distance between the two wires is R, and we are interested in the magnetic field at a point P that is located midway between the two wires.
Step 2: Determine the Distance from Each Wire
Since point P is midway between the two wires, the distance from each wire to point P is:
\(
d = \frac{R}{2}
\)
Step 3: Use the Formula for Magnetic Field
The magnetic field B due to a long straight wire carrying current I at a distance d from the wire is given by the formula:
\(
B = \frac{\mu_0 I}{2 \pi d}
\)
where μ₀ is the permeability of free space.
Step 4: Calculate the Magnetic Field from Each Wire
For Wire 1, the magnetic field at point P (due to current I flowing in one direction) is:
\(
B_1 = \frac{\mu_0 I}{2 \pi \left(\frac{R}{2}\right)} = \frac{\mu_0 I}{\pi R}
\)
For Wire 2, the magnetic field at point P (due to current I flowing in the opposite direction) is:
\(
B_2 = \frac{\mu_0 I}{2 \pi \left(\frac{R}{2}\right)} = \frac{\mu_0 I}{\pi R}
\)
Step 5: Determine the Direction of the Magnetic Fields
Since the currents are in opposite directions, the magnetic fields at point P due to each wire will be in the same direction (into the plane of the paper). Therefore, we can add the magnitudes of the magnetic fields from both wires.
Step 6: Calculate the Net Magnetic Field
The net magnetic field B≠t at point P is:
\(
B_{net} = B_1 + B_2 = \frac{\mu_0 I}{\pi R} + \frac{\mu_0 I}{\pi R} = \frac{2 \mu_0 I}{\pi R}
\)
Conclusion
Thus, the magnetic induction at the point midway between the two wires is:
\(
B_{net} = \frac{2 \mu_0 I}{\pi R}
\)
We have two long straight wires, Wire 1 and Wire 2, each carrying a current I in opposite directions. The distance between the two wires is R, and we are interested in the magnetic field at a point P that is located midway between the two wires.
Since point P is midway between the two wires, the distance from each wire to point P is:
\(
d = \frac{R}{2}
\)
The magnetic field B due to a long straight wire carrying current I at a distance d from the wire is given by the formula:
\(
B = \frac{\mu_0 I}{2 \pi d}
\)
where μ₀ is the permeability of free space.
For Wire 1, the magnetic field at point P (due to current I flowing in one direction) is:
\(
B_1 = \frac{\mu_0 I}{2 \pi \left(\frac{R}{2}\right)} = \frac{\mu_0 I}{\pi R}
\)
For Wire 2, the magnetic field at point P (due to current I flowing in the opposite direction) is:
\(
B_2 = \frac{\mu_0 I}{2 \pi \left(\frac{R}{2}\right)} = \frac{\mu_0 I}{\pi R}
\)
Since the currents are in opposite directions, the magnetic fields at point P due to each wire will be in the same direction (into the plane of the paper). Therefore, we can add the magnitudes of the magnetic fields from both wires.
The net magnetic field B≠t at point P is:
\(
B_{net} = B_1 + B_2 = \frac{\mu_0 I}{\pi R} + \frac{\mu_0 I}{\pi R} = \frac{2 \mu_0 I}{\pi R}
\)
Thus, the magnetic induction at the point midway between the two wires is:
\(
B_{net} = \frac{2 \mu_0 I}{\pi R}
\)
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Video
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Video
Similar Questions
The two long, straight wires carrying electric currents in opposite directions. The separation between the wires is 5.0 cm. Find the magnetic field at a point P midway between the wires.
View SolutionTwo long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View Solution
Knowledge Check
Two long and parallel straight wires A and B are carrying currents of 4A and 7A in the same directions are separated by a distance of 5cm. The force acting on a 8cm section of wire A is
A3×10−6NB6×10−6NC9×10−6ND12×10−6N
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
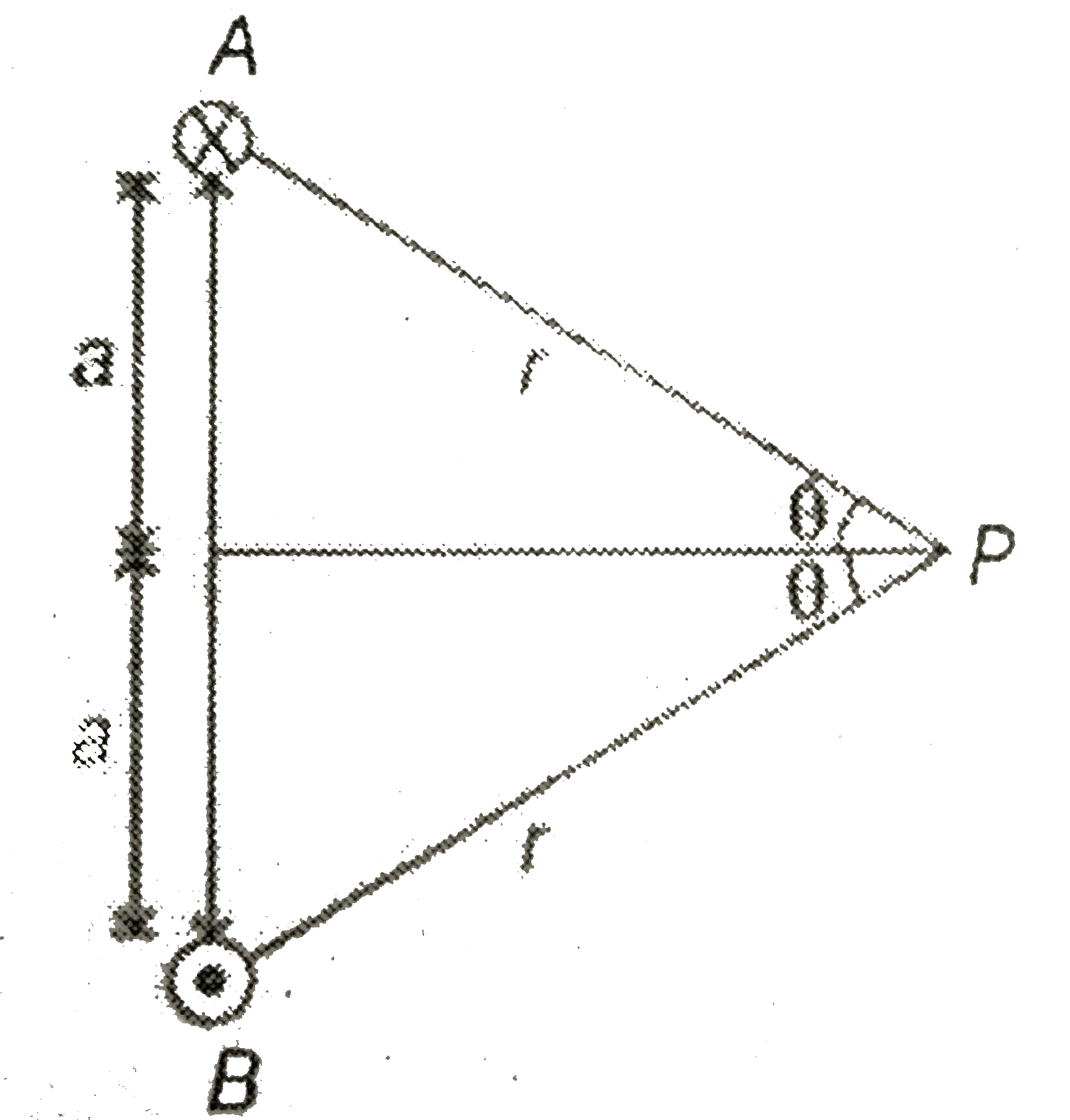
View SolutionTwo long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
View SolutionTwo long parallel conductors carry currents I and 2I in the same direction. The magnetic induction at a point exactly mid way between them is B. If the current in the first conductor is reversed in direction, the magnetic induction at the same point will be
View SolutionTwo infinitely long straight parallel wires carry equal currents 'I' in the same direction and are 2 m apart. Magnetic induction at a point which is at same normal distance (√2)m from each wire has magnitude
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionTwo long and parallel straight wires A and B carrying currents of 8⋅0A and 5⋅0A in the same direction are separated by a distance of 4⋅0cm. Estimate the force on a 10cm section of wire A.
View Solution