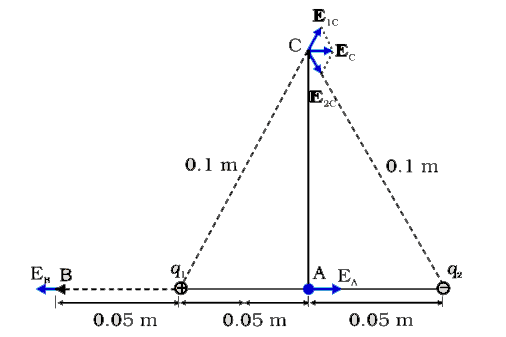
Two point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.
EA=7.2×104NC−1 EB=3.2×104NC−1
EB is directed towards the RIGHT.
EA=7.2×10−4NC−1 EB=3.2×104NC−1
EB is directed towards the left.
EA=7.2×104NC−1 EB=3.2×104NC−1
EB is directed towards the left.
EA=7.2×104NC−1 EB=3.2×10−4NC−1
EB is directed towards the left.
The correct Answer is:C
The electric field vector E1A at A due to the positive charge q1 points towards the right and has a magnitude
E1A=(9×109NmC2)×(10−8C)(0.05m2)=3.6104NC−1
The electric field vector E2A at A due to the negative charge q2 points towards the right and has the same magnitude. Hence the magnitude of the total electric field EA at A is
EA=E1A+E2A=7.2×104NC−1
EA is directed toward the light.
The electric field vector E1B at B due to the positive charge q1 points towards the left and has a magnitude
E1B=(9×109Nm2C−2)×(10−8C)(0.05m)2=3.6×104NC−1
The electric field vector E2B at B due to the negative charge q2 points towards the right and has a magnitude
E1B=(9×109Nm2C−2)×(10−8C)(0.15m)2=4×103NC−1
The magnitude of the total electric field at B is
EB=E1B−E2B=3.2×104NC−1
EB is directed towards the left.
The directions in which these two vectors point are indicated in Fig. 1.14. The resultant of these two vectors is
EC=E1cos(π)3+E2Cosπ3=9×10−3NC−1
Ec points towards the right.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise34videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NCERT ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - All Questions32videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise17videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two point charges +10−7C and −10−7C are placed at A and B 20 cm apart as shown in the figure. Calculate the electric field at C, 20 cm apart from both A and B.
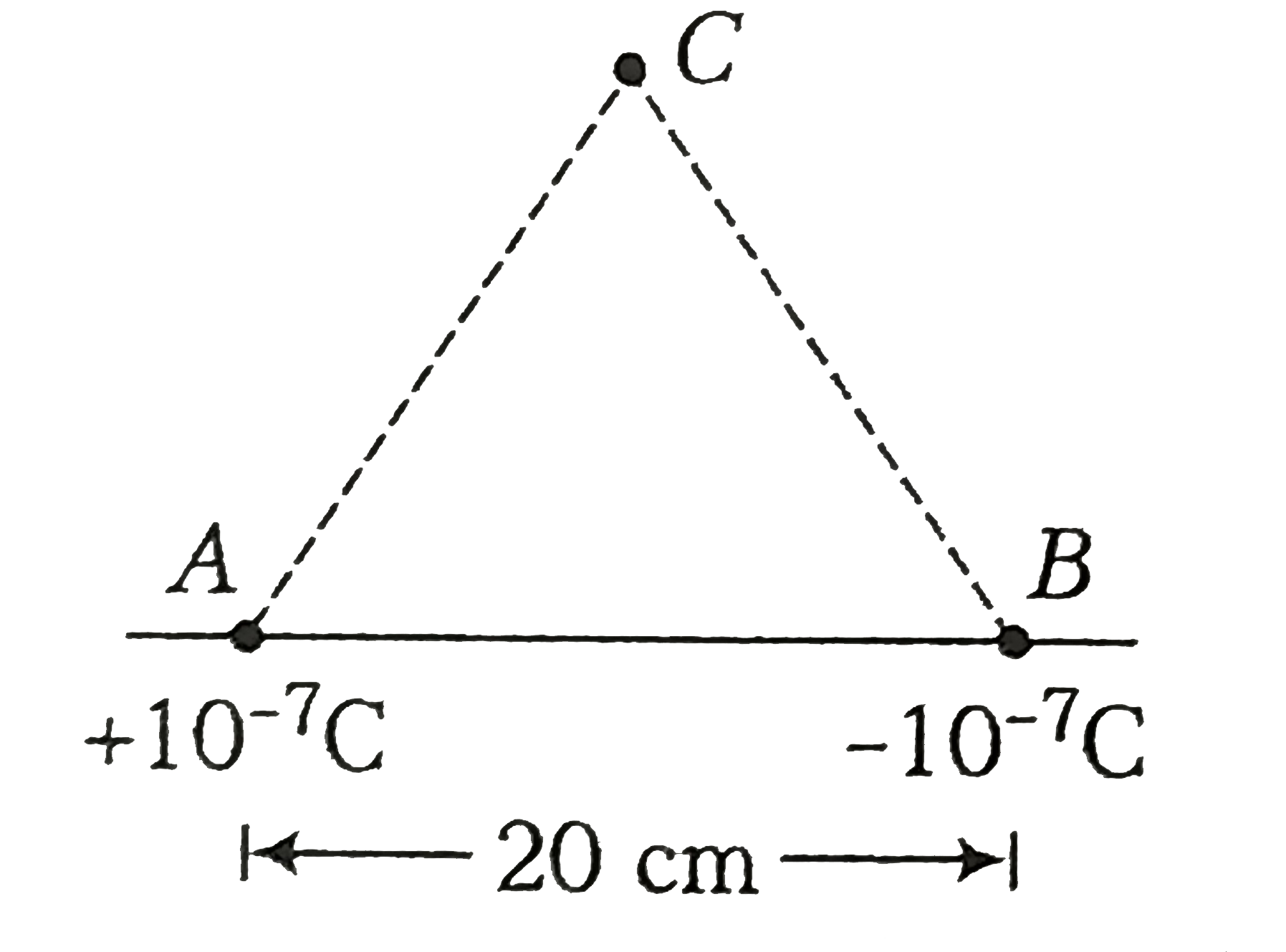 View Solution
View SolutionTwo point charges qA=3μC and qB=−3μC are located 20 cm apart in vaccum (a) what is the electric field at the mid point O of the line AB joining the two charges ? (b) If a negative test charge of magnitude 1.5×10−9C is placed at the point, what is the force experienced by the test charge ?
View SolutionTwo point charges qA=3μCandqB=−3μC are located 20cm apart in vacuum. What is the electric field at the mid point of the line joining the two charges.
 View Solution
View SolutionTwo charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
View SolutionIn figure, the charges on C1,C2, and C3, are Q1,Q2, and Q3, respectively.
 .View Solution
.View SolutionThree large identical conducting parallel plates carrying charge +Q,−Q,and+2Q, respectively, are placed as shown in figure. If EA,Eb,andEC refer to the magnitudes of the electric field at points A, B, and C, respectively. Then
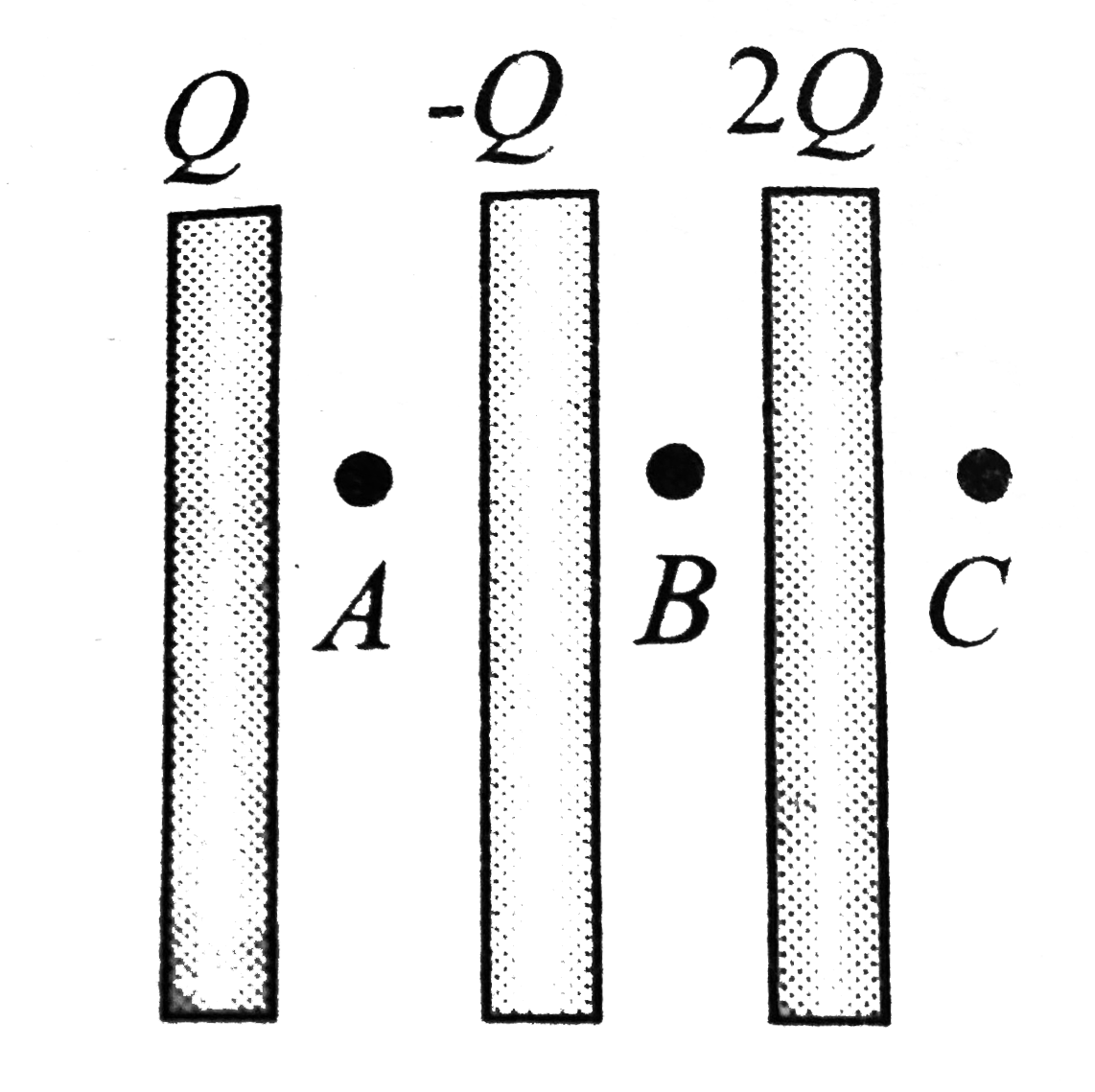 View Solution
View SolutionTwo point charges Q1=400μCand Q2=100μC are kept fixed, 60 cm apart in vacuum. Find intensity of the electric field at midpoint of the line joining Q1 and Q2.
View SolutionTwo charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionThe positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
View Solution

