Two charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
4.5×106NC−1 directed towards +5μC
4.5×106NC−1 directed towards +10μC
13.5×106NC−1 directed towards +5μC
13.5×106NC−1 directed towards +10μC
The correct Answer is:A
To find the net electric field at the midpoint between two charges +5μC and +10μC placed 20cm apart, we can follow these steps:
Step 1: Identify the positions of the charges
Let’s denote the charges as:
- Charge Q1=+5μC located at point A.
- Charge Q2=+10μC located at point B.
The distance between the two charges is 20cm, which means the midpoint (point M) is 10cm from both charges.
Step 2: Calculate the electric field due to each charge at the midpoint
The electric field E due to a point charge is given by the formula:
E=k⋅|Q|r2
where:
- k=9×109N⋅m2/C2 (Coulomb's constant),
- Q is the charge,
- r is the distance from the charge to the point where the field is being calculated.
Electric Field due to Q1 at M:
- Distance r1=10cm=0.1m
- Charge Q1=+5μC=5×10−6C
Calculating E1:
E1=9×109⋅5×10−6(0.1)2=9×109⋅5×10−60.01=4.5×106N/C
This electric field is directed away from Q1 (to the right, along the positive x-axis).
Electric Field due to Q2 at M:
- Distance r2=10cm=0.1m
- Charge Q2=+10μC=10×10−6C
Calculating E2:
E2=9×109⋅10×10−6(0.1)2=9×109⋅10×10−60.01=9×106N/C
This electric field is also directed away from Q2 (to the left, along the negative x-axis).
Step 3: Determine the direction of the net electric field
Since both charges are positive, the electric field due to Q1 (to the right) and Q2 (to the left) will oppose each other. Therefore, the net electric field will be directed towards the charge with the smaller magnitude, which is Q1.
Step 4: Calculate the net electric field
The net electric field Enet at the midpoint is given by:
Enet=E2−E1
Substituting the values:
Enet=9×106−4.5×106=4.5×106N/C
This net electric field is directed towards Q1.
Final Answer
The net electric field at the midpoint between the two charges is:
Enet=4.5×106N/C(towards +5μC)
Let’s denote the charges as:
- Charge Q1=+5μC located at point A.
- Charge Q2=+10μC located at point B.
The electric field E due to a point charge is given by the formula:
E=k⋅|Q|r2
where:
- k=9×109N⋅m2/C2 (Coulomb's constant),
- Q is the charge,
- r is the distance from the charge to the point where the field is being calculated.
- Distance r1=10cm=0.1m
- Charge Q1=+5μC=5×10−6C
E1=9×109⋅5×10−6(0.1)2=9×109⋅5×10−60.01=4.5×106N/C
This electric field is directed away from Q1 (to the right, along the positive x-axis).
- Distance r2=10cm=0.1m
- Charge Q2=+10μC=10×10−6C
E2=9×109⋅10×10−6(0.1)2=9×109⋅10×10−60.01=9×106N/C
This electric field is also directed away from Q2 (to the left, along the negative x-axis).
Since both charges are positive, the electric field due to Q1 (to the right) and Q2 (to the left) will oppose each other. Therefore, the net electric field will be directed towards the charge with the smaller magnitude, which is Q1.
The net electric field Enet at the midpoint is given by:
Enet=E2−E1
Substituting the values:
Enet=9×106−4.5×106=4.5×106N/C
This net electric field is directed towards Q1.
The net electric field at the midpoint between the two charges is:
Enet=4.5×106N/C(towards +5μC)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.2
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A and B are two points separately by a distance 5cm. Two charges 10μCand20μC are placed at A and B. The resultant electric intensity at a point P outside the charges at a distance 5cm from 10μC is
View SolutionTwo tiny spheres carrying charges 1.5μC and 2.5μC are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View Solution
Knowledge Check
Two tiny spheres carrying charges 1.8μCand2.8μC are located at 40 cm apart. The potential at the mid-point of the line joining the two charges is
A3.8×104VB2.1×105VC4.3×104VD6.3×105V
Two charges +20μCand−20μC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
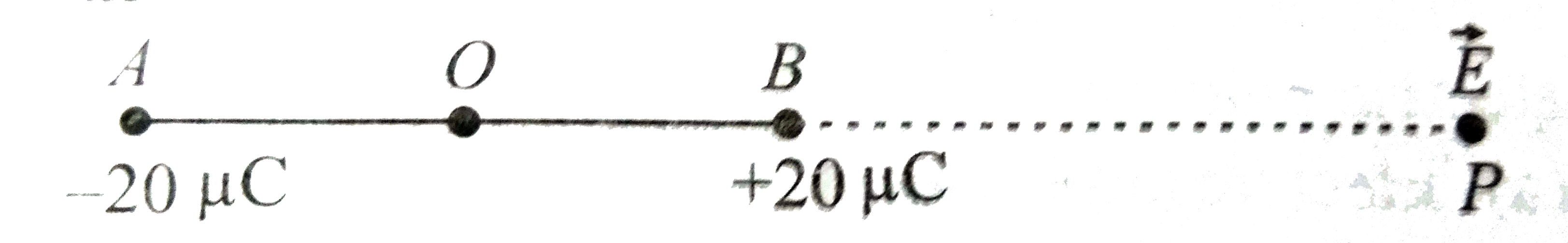
View SolutionTwo point charges qA=3μCandqB=−3μC are located 20cm apart in vacuum. What is the electric field at the mid point of the line joining the two charges.

View SolutionTwo point charge - 5μC and + 3μC are placed 64 cm apart. At what points on the line joining the two charges is the electric potential zero. Assume the potential at infinity to be zero.
View SolutionTwo charges -4 μC and 8 μC are 27 cm apart. The distance from the first charge on line of joining between two charges where electric potential would be zero is
View SolutionTwo charges +20μCand−20μC are held 1cm apart. Calculate the electric field at a point on the equatorial line at a distance of 50cm from the center of the dipole.
View SolutionTwo point charges of 20μC and 80μC are 10 cm apart where will the electric field strength be zero on the line joining the charges from 20μC charge
View SolutionTwo electric charges 12μC and −6μC are placed 20cm apart in air. There will be a point P on the line joining these charges and outside the region between them, at which the electric potential is zero. The distance of P from 6μC charge is
View Solution
