Two point masses m and 2m are kept at points A and B as shown. E represents magnitude of gravitational field strength and V the gravitational potential. As we move from A to B

E will first decreases then increases
E will first increases then decreases
V will first decreases then increases
V will first increases then decrease
The correct Answer is:A, D
E due to point mass is E=Gmr2
As r→0,E→∝
So, just over the point masses, E=∞. Hence, in moving from one point mass to other point mass, E first decreases and then increases.
V due to a point mass is
V=−Gmr
As r→0,V→−∞
So, just over the point mass, V is −∞. Hence, in moving from one point mass to other point mass, V first increase and then decrease .
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.1
20 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Three point masses 'm' each are kept at three verties of a square pf side 'a' as shown in figure. Find gravitation potential and field strength at point O.
 .
.
View SolutionTwo point masses 100 kg and 25 kg are situated at two points 2 m apart, then the gravitational potential midway between them will be
View Solution
Knowledge Check
In a gravitational field, at a point where the gravitational potential is zero
AThe gravitational field is necessarily zeroBThe gravitational field is not necessarily zeroCNothing can be said definitely about the gravitational fieldDNone of theseThe magnitude of the gravitational potential at point O will be
AGm2rBGmrC3Gm2rD2GmrTwo bodies of masses M1 and M2, are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
A−G√M1RB−G√M2RC−(√M1+√M2)2GRD−(√M1−√M2)2GR
Two particle of masses 4kg and 8kg are kept at x=−2m and x=4m respectivley. Then, the gravitational field intensity at the origin is
View SolutionAt some point the gravitational potential and also the gravitational field due to earth is zero. The point is
View SolutionTwo particles of masses 'm' and '9m' are separated by a distance 'r'. At a point on the line joining them the gravitational field is zero. The gravitational potential at that point is (G = Universal constant of gravitation)
View SolutionFour identical masses m each are kept at points A, B, C & D shown in figure. Gravitational force on mass at point D (body centre) is -
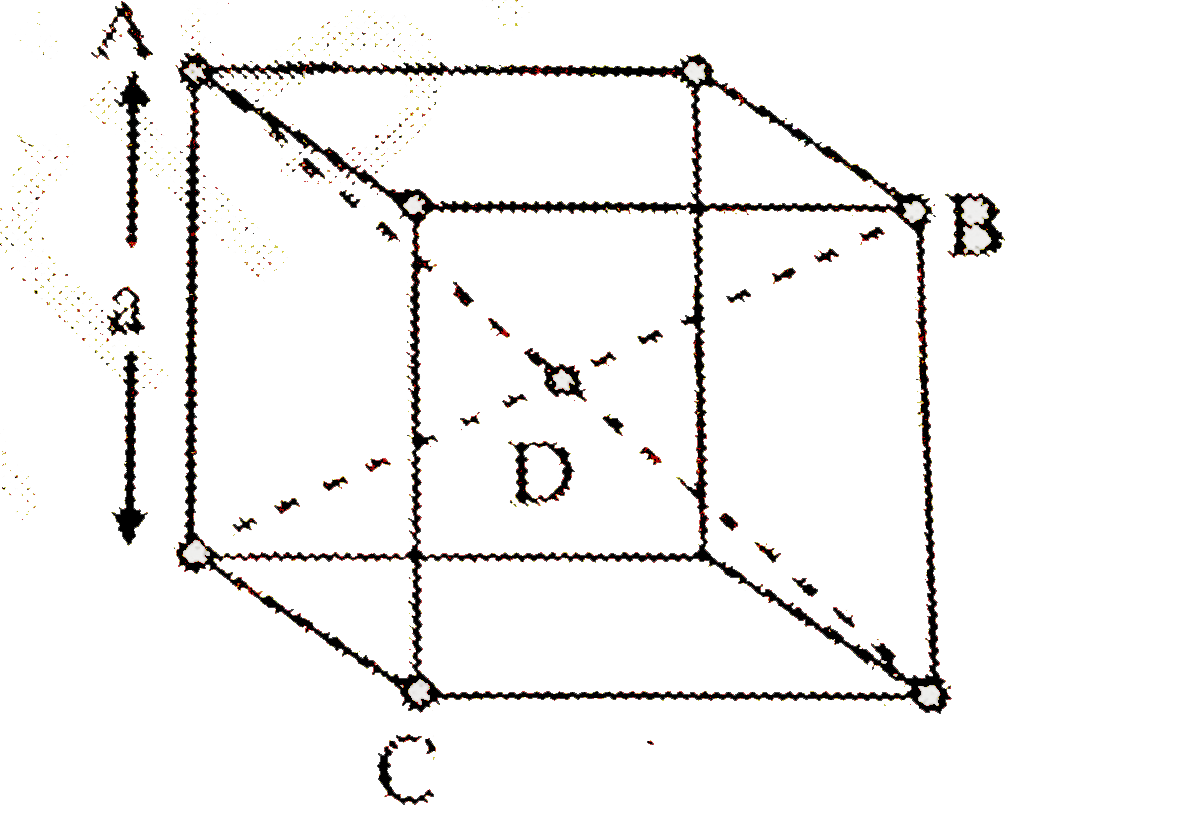
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
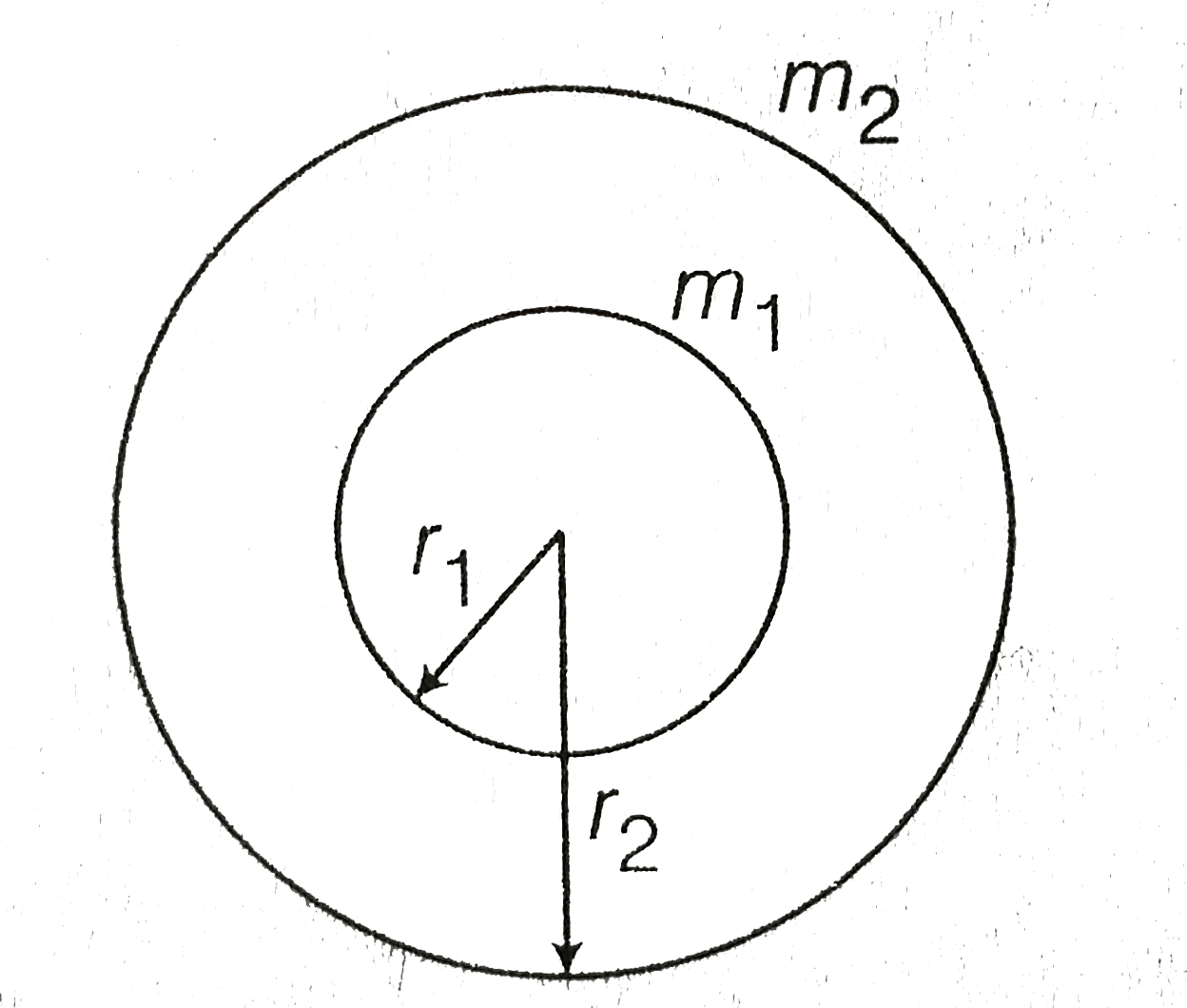
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View Solution
