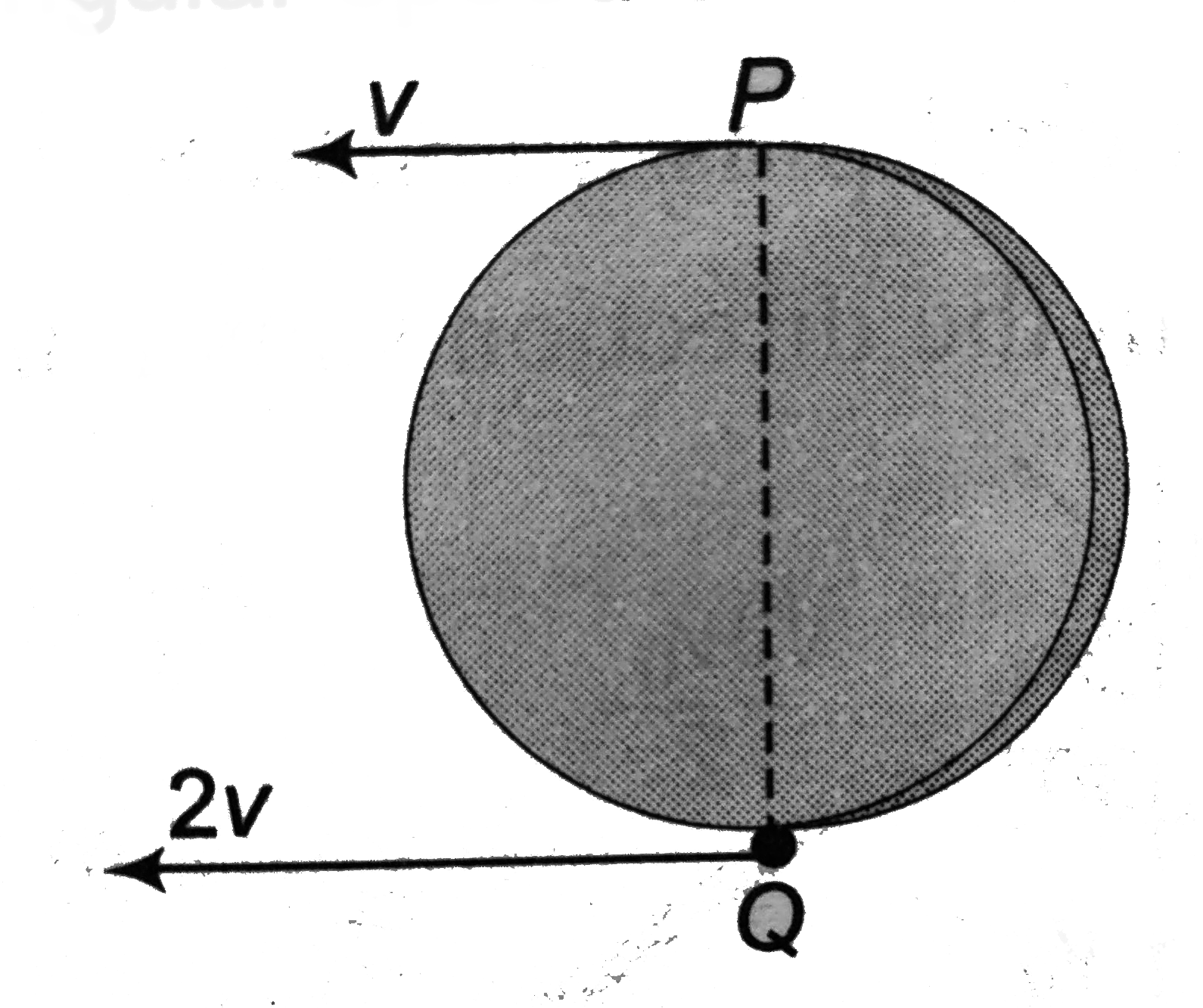
Two point P and Q. diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.
ω=−vrPQ=2v−v2R=v2R
Rotation is clockwise So, ω is perpendicular to paper inward.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.3
4 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.4
11 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.1
10 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
View SolutionA particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View Solution
Knowledge Check
A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
 A52mR2ω about OB72mR2ω about OC12mR2ω about AD4mR2ω about A
A52mR2ω about OB72mR2ω about OC12mR2ω about AD4mR2ω about AA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is
 A3V2R AnticlockwiseB3V2R ClockwiseCV2R AnticlockwiseDV2R clockwise
A3V2R AnticlockwiseB3V2R ClockwiseCV2R AnticlockwiseDV2R clockwiseA solid sphere is set into motion on a rough horizontal surface with a linear velocity v in the forward direction and an angular velocity v/R in the anticlockwise direction as shown in the figure. Find the linear speed of the sphere, when it stops rotating.
 Av5Bv7C3v5D3v7
Av5Bv7C3v5D3v7
In the figure (i) a disc of mass M(kg) and radius R(m) is rotating smoothly about a fixed vertical axis AB with angular speed 26rad/s A rod rod CD of length R2(m) and mass M(kg) is hinged at one end at point 'D' on the disc. The rod remains in vertical position and rotates along with the disc about axis AB. At some moment the rod CD gets a very smal impulse at point 'C' due to air due to which the rod falls on the disc along one radius and sticks to the disc as shown in figure (ii). Now find the angular velocity of the disc in rad/s.

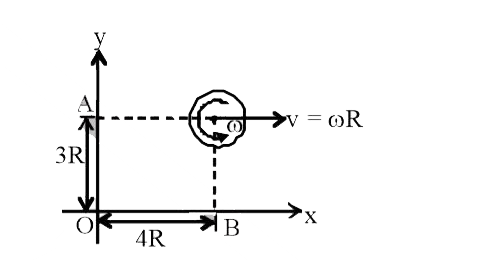
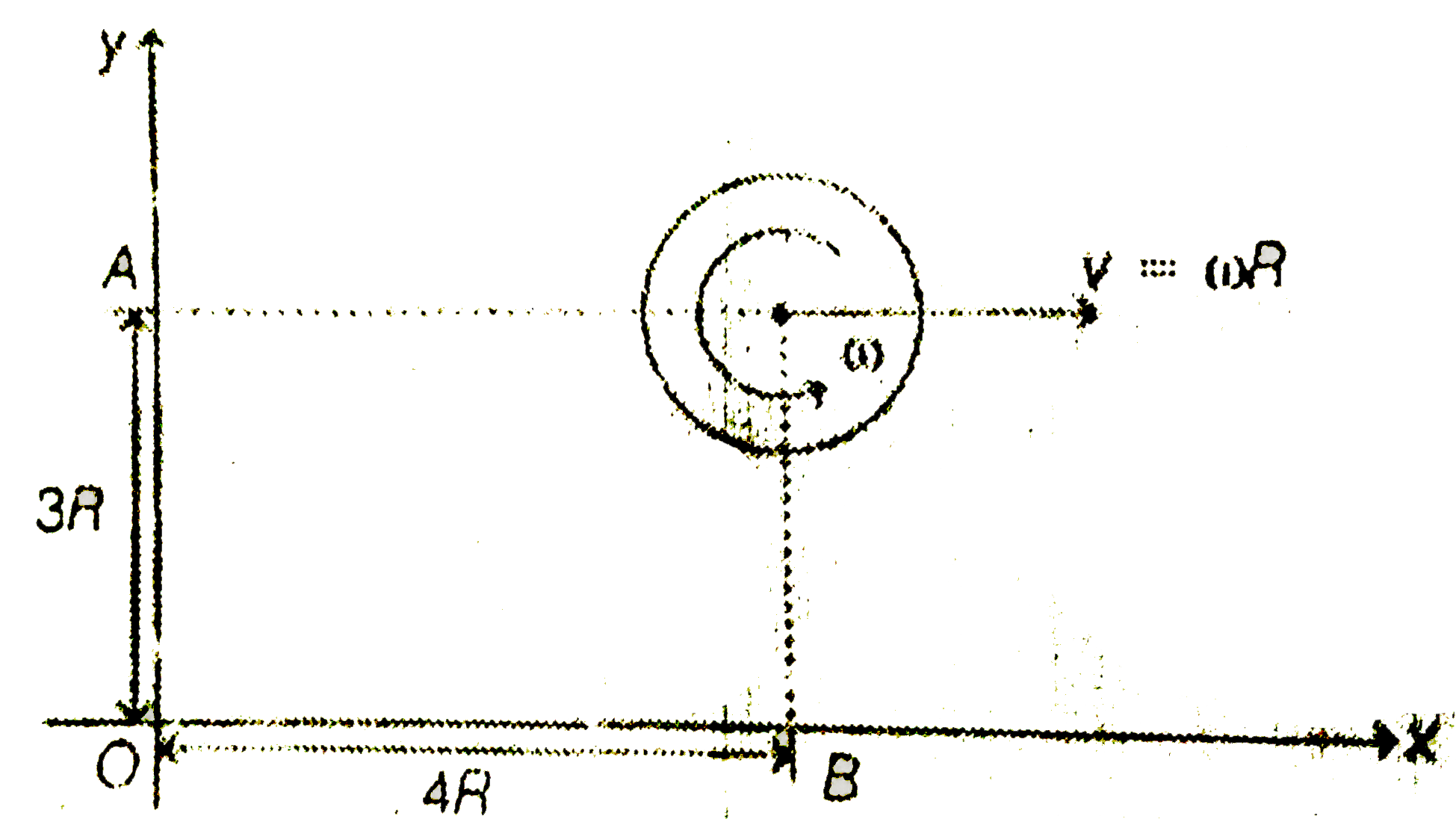
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis through its centre about which it can freely rotate. The man starts to move around the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.
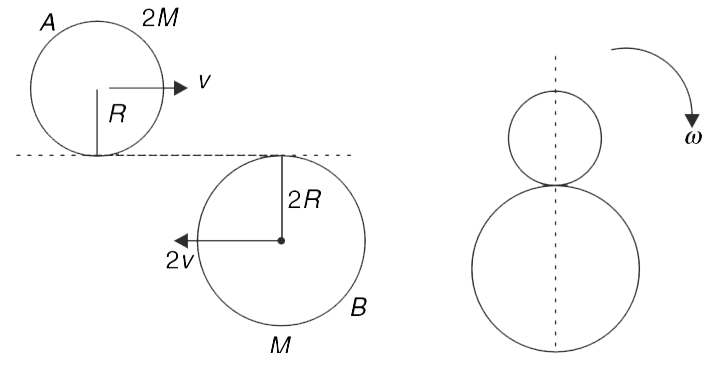
View SolutionTwo discs A and B are moving with their flat circular surface on a smooth horizontal surface. Mass, radius and velocity of the two discs are −mA=2M,mB=M,rA=R,=2R,vA=v, and vB=2v. The velocities of the two discs are oppositely directed so that they just cannot avoid collision and stick to each other (see figure)
(a) Find the angular speed of the composite system after collision
(b) Find loss in kinetic energy due to collision
View Solution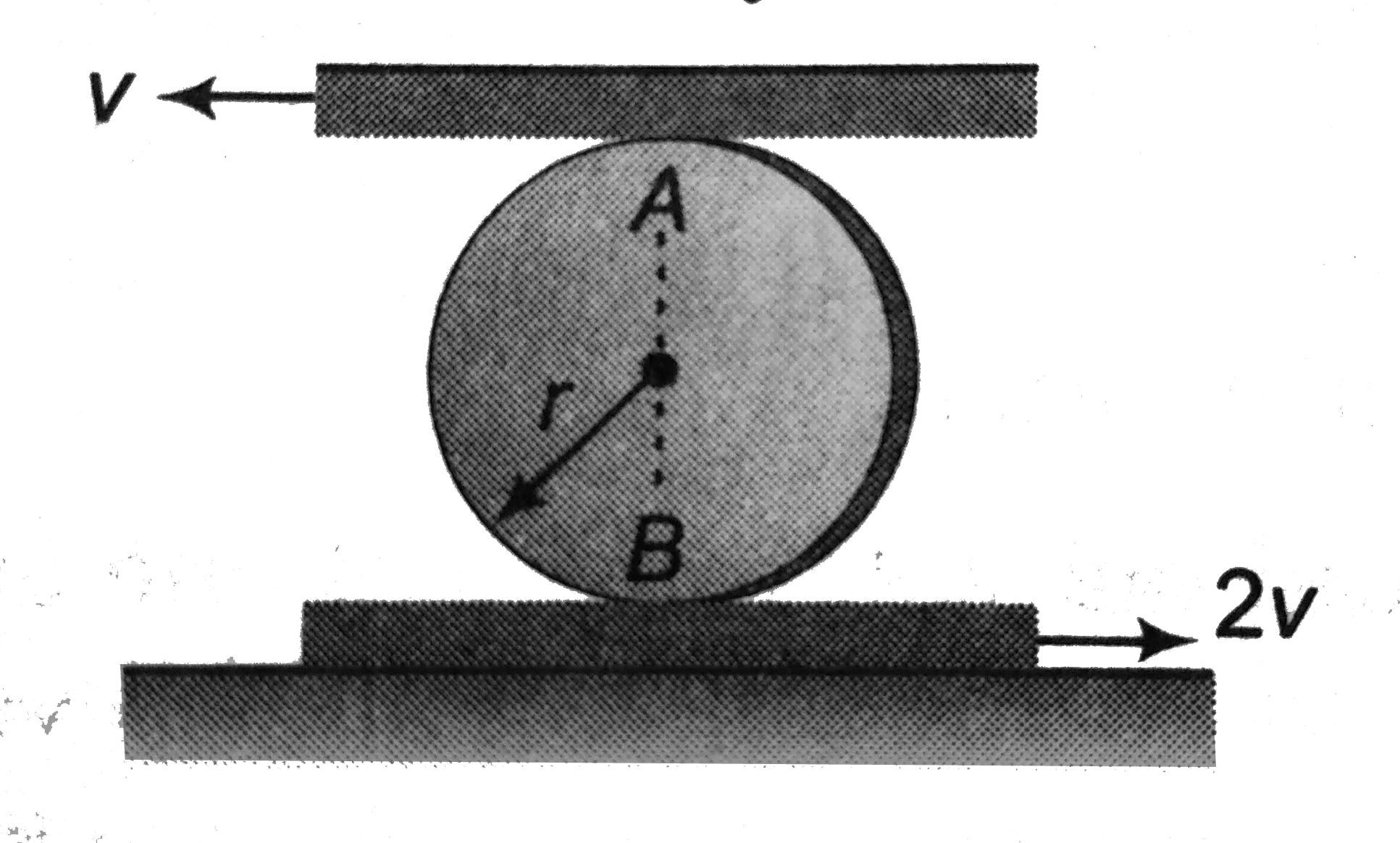
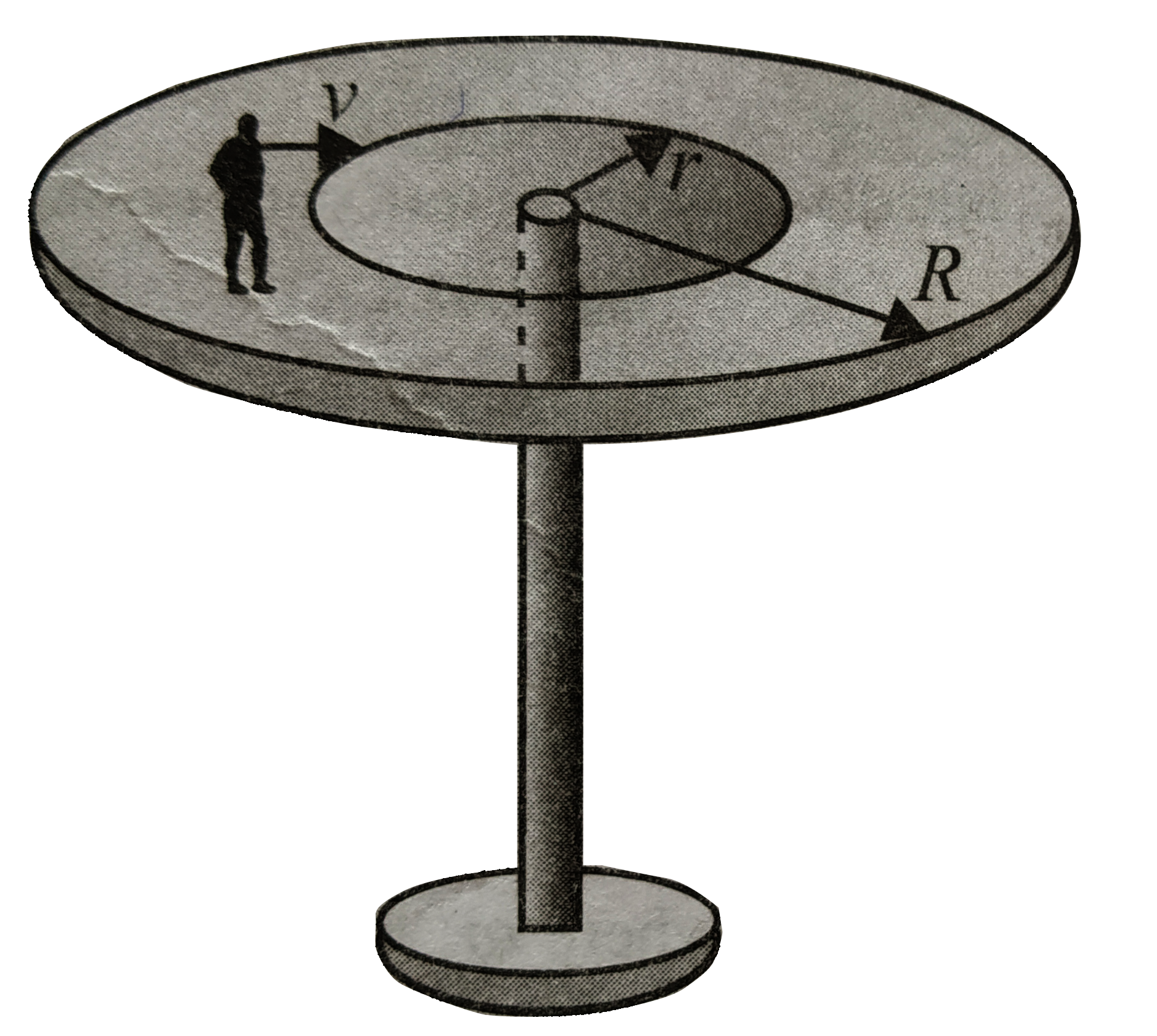
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View Solution
Particle P shown in figure is moving in a circle of radius R=10 cm with linear speed v=2m/s Find the angular speed of particle about point O.
View Solution
