A particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

We see that impact takes place along the normal. Therefore, the particle and the disc change their momentum along that line. However, no external force acts on the system along the norma line. Hence we can conserve the linear momentum of the system (disc+particle) along the normal. Since the masses of the disc and particle are equal, so the exchange of momentum takes place along the normal. That means, the particle completely delivers the part (component) of its momentum (m vcosθ) along the normal
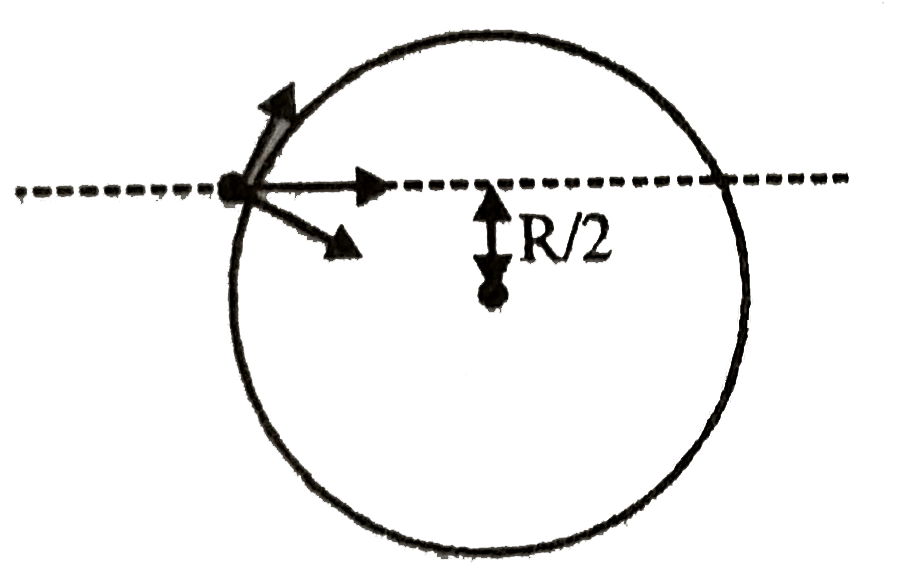
⇒ Velocity of the disc, →∨1=(vcosθ)ˆj where, cosθ=cos30∘=√32
⇒ →v1=√3v2ˆj
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Practice Exercise
20 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]
23 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
8 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
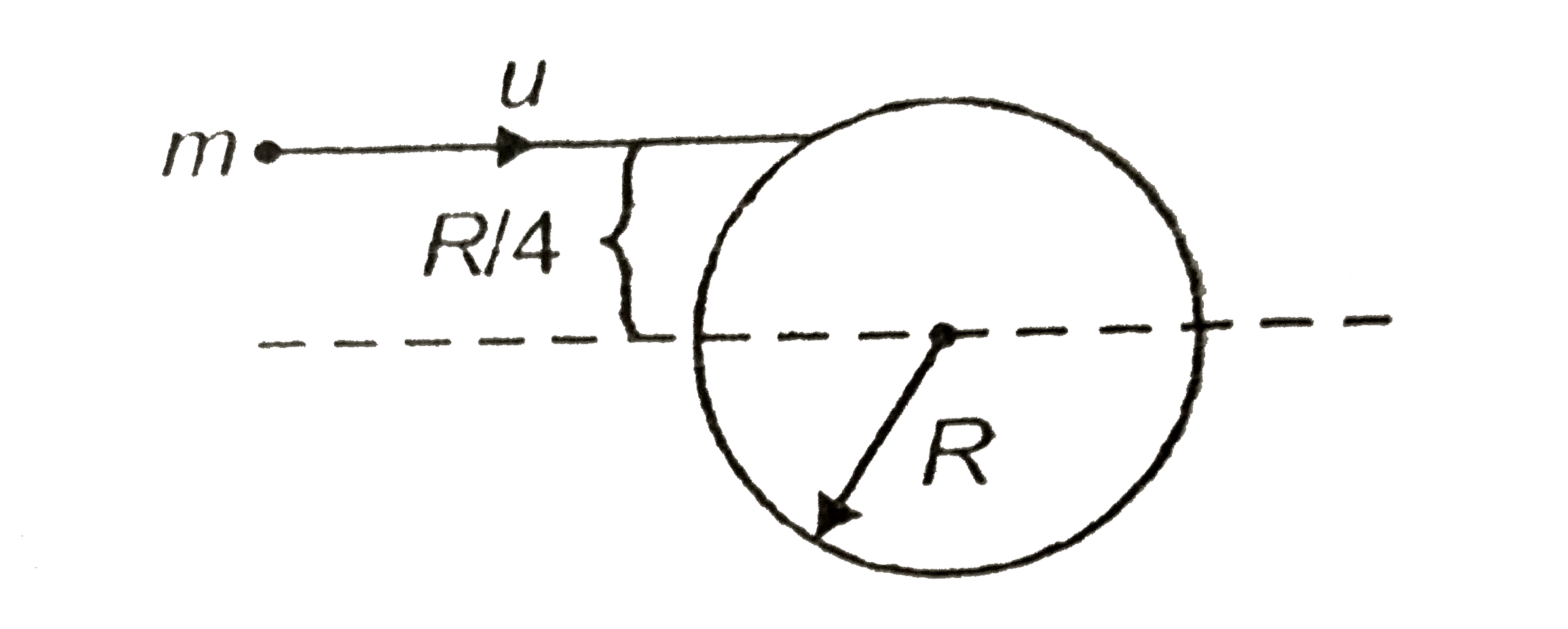
A particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View SolutionA particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
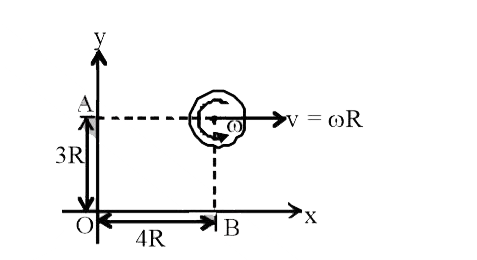
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
View SolutionA particle (a mud pallet, say) of mass m strikes a smooth stationary wedge of mass M with as velocity v0 at an angle θ with horizontal. If the collision is perfectly inelastic, find the
a. velocity of the wedge just after the collision.
b. Chane in KE of the system (M+m) in collision.
View SolutionThree identical discs A, B, and C (figure) rest on a smooth horizontal plane. The disc A is set in motion with vector v after which it experiences an elastic collision simultaneously with the discs B and C. The distance between the centres of the latter discs prior of the collision is η times greater than the diameter of each disc.
Find the velocity of the disc A after the collision. At what value of η will the disc A recoil after the collision, stop, move on?

View SolutionA small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
View SolutionA bullet of mass m collides inelastically at the periphery of a disc of mass M and radius R, with a speed v as shown. The disc rotates about a fixed horizontal axis. Find the angular velocity of the disc bullet system just after the impact.

View SolutionA particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
View Solution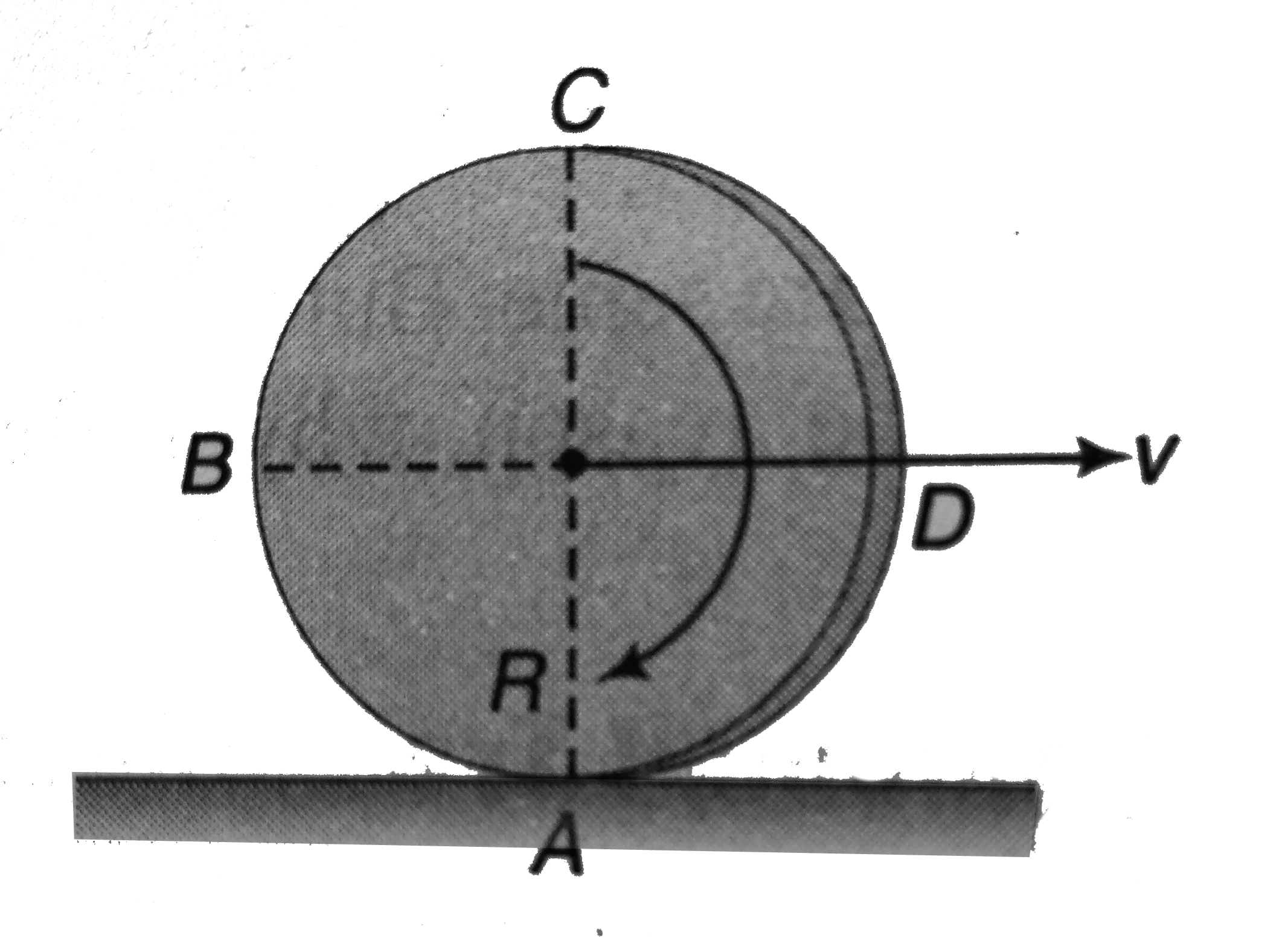
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View Solution
