Two pulses having equal and opposite displacements
moving in oppositee directions overlap at sec.
The resultant displacement of the wave at sec is
twice the displacement of each pulse
half the displacement of each pulse
zero
Either (a) or (c )
The correct Answer is:c
To solve the problem of two pulses having equal and opposite displacements moving in opposite directions, we can follow these steps:
1. Understand the Pulses: We have two pulses that are equal in amplitude but have opposite displacements. Let's denote the amplitude of the first pulse as A (moving in the positive direction) and the second pulse as −A (moving in the negative direction).
2. Identify the Time of Overlap: The pulses overlap at t=t1 seconds. At this moment, we need to find the resultant displacement of the wave.
3. Apply the Principle of Superposition: According to the principle of superposition, when two waves overlap, the resultant displacement is the algebraic sum of the individual displacements.
yresultant=y1+y2
Here, y1=A (displacement of the first pulse) and y2=−A (displacement of the second pulse).
4. Calculate the Resultant Displacement: Substitute the values of y1 and y2 into the equation:
yresultant=A+(−A)=A−A=0
5. Conclusion: The resultant displacement of the wave at t=t1 seconds is 0.
Final Answer:
The resultant displacement of the wave at t=t1 seconds is 0.
---
The resultant displacement of the wave at t=t1 seconds is 0.
Topper's Solved these Questions
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - EXERCISE 2
27 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- SEMICONDUCTORSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEMICONDUCTORSEXERCISE - MHT CET Corner
25 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
Similar Questions
A sonometer wire of length 1.5m is made of steel. The tension in it produces an elastic strain of 1%. What is the fundamental frequency of steel if density and elasticity of steel are 7.7×103kg/m3 and 2.2×1011N/m2 respectively ?
View SolutionTwo strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed vA and on B with speed vB. The ratio vAvB is
View SolutionTwo strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed vA and on B with speed vB. The ratio vAvB is
View SolutionThe schematic symbol of light emitting diode (LED) is
View SolutionIn a capillary tube of radius 'R' a straight thin metal wire of radius 'r' (R>r) is inserted symmetrically and one of the combination is dipped vertically in water such that the lower end of the combination Is at same level . The rise of water in the capillary tube is [T=surface tensiono of water ρ =density of water ,g =gravitational acceleration ]
View SolutionTwo equal spheres A and B lie on a smooth horizontal circular groove at opposite ends of a diameter. At time t=0, A is projected along the groove and it first impinges on B at time t=T1 and again at time t=T2. If e is the coefficient of restitution, the ratio T2/T1 is
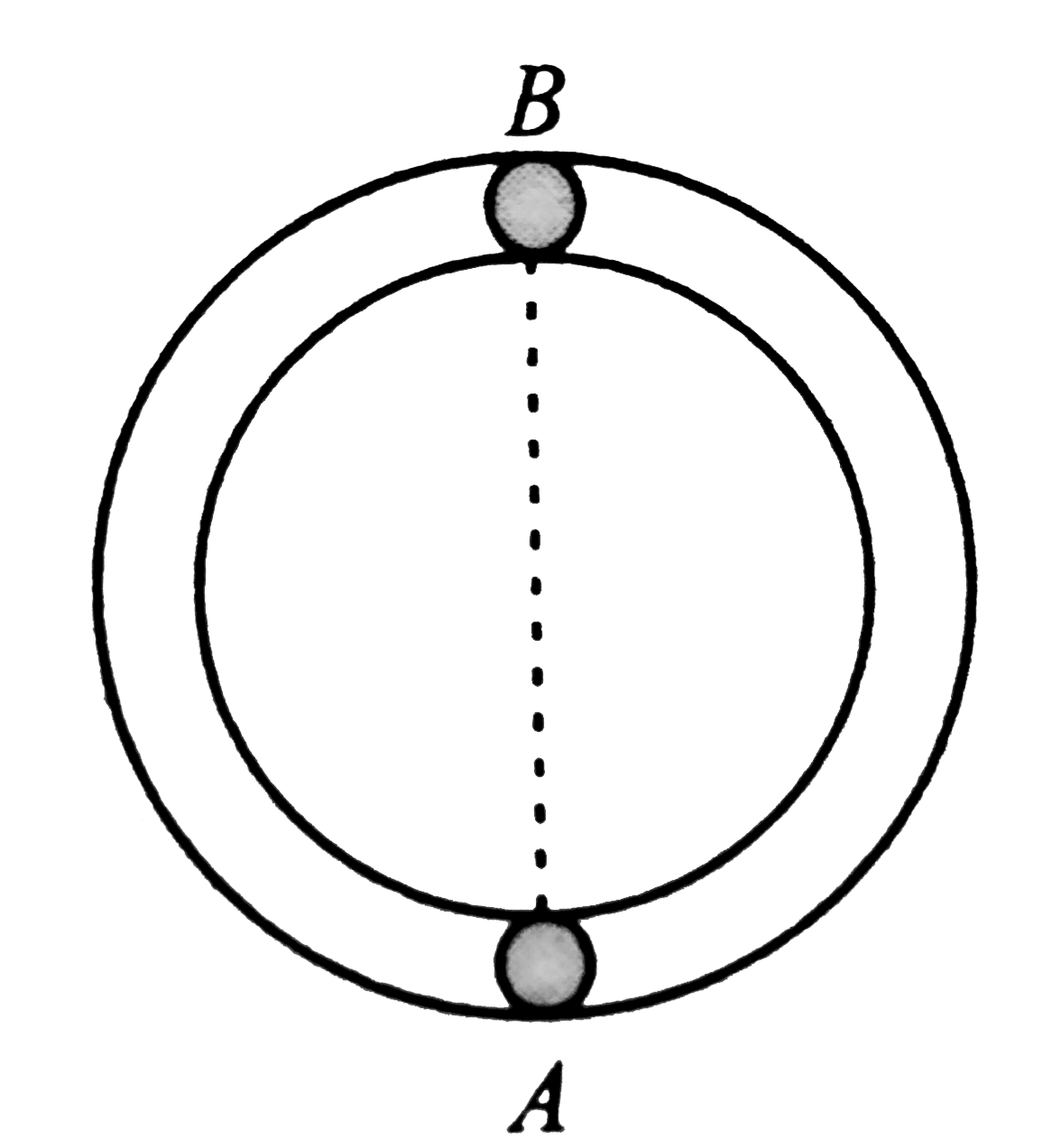
View SolutionTwo equal sphere A and b lie on a smooth horizontal circle groove at opposite ends of a diameter. At time t= 0,A is projected along the groove and tis first implings on B at time t = T_(1) and again at time t = T_(2). If e is the coefficient of restitution, the ratio T_(2)//T_(1) is
View SolutionThe angular displacement of a particle is given by θ=t3+t2+t+1 then, its angular velocity at t=2 sec is …… rads−1
View SolutionThe bae of a triangle is divided into three equal parts. If t1,t2,t3 be the tangent sof the angles subtended by these parts at the opposite vertex, prove that :
(1t1+1t2)(1t1+1t3)=4(1+1t21)
View SolutionIf 't1','t2'and't3' are the lengths of the tangents draen from centre of x-circle to the circumcircle of the ΔABC, then 1t21+1t22+1t23 is equal to
View SolutionIf displacement S at time t is S=t3−3t2−15t+12, then acceleration at time t=1sec is
View Solutiont_(x//y) = time in which x//y fraction of reactant converts into product. {:(,"Column-I",,"Column-II"),("(a)",t_(5//9),,(p)Equal t o 54 sec if t_(1//3) "is 18 sec in case of first order reaction"),("(b)",t_(19//27),,(q)Equal t o 32 sec if t_(1//14) "is 16 sec in case of first order reaction"),("(c)",t_(7//8),,(r)Equal t o 56 sec if t_(1//3) "is 4 sec in case of second order reaction"),("(d)",t_(7//16),,(t)Equal t o 30 sec if t_(1//3) "is 18 sec incase of zero order reaction"),(,,,(t)Equal t o 28 sec if t_(1//2) "is 16 sec in case of zero order reaction"):}
View SolutionIn the above question, the displacement of particle at t = 1 sec and x = 4 cm is:
View SolutionTwo equal spheres A and B lie on a smooth horizontal circular groove at opposite ends of a diameter. At time t = 0, A is projected along the groove and it first impinges on B at time t = T_(1) and again at time t = T_(2) . If .e. is the coefficient of restitution, find the ratio of T_(2)//T_(1)
View SolutionAt two particular closest instants of time t1 and t2, the displacements of a particle performing SHM are equal. At these instants.
View Solution
