The bae of a triangle is divided into three equal parts. If t1,t2,t3 be the tangent sof the angles subtended by these parts at the opposite vertex, prove that :
(1t1+1t2)(1t1+1t3)=4(1+1t21)
The correct Answer is:4(1+1t22)=(1t1+1t1)(1t2+1t2)
Step by step video, text & image solution for The bae of a triangle is divided into three equal parts. If t_(1), t_(2), t_(3) be the tangent sof the angles subtended by these parts at the opposite vertex, prove that : ((1)/(t_(1))+ (1)/(t_(2)))((1)/(t _(1))+(1)/(t _(3)))=4(1+(1)/(t_(1)^(2))) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 120videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 219videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)52videos
PRODUCT OF VECTORS
- BOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)38videos
SEQUENCES AND SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
If 't1','t2'and't3' are the lengths of the tangents draen from centre of x-circle to the circumcircle of the ΔABC, then 1t21+1t22+1t23 is equal to
Aabca+b+cBa+b+cabcCa+b+c2abcD2abca+b+c
If A, B, C, be the centres of three co-axial circles and t1,t2,t3 be the lengths of the tangents of them any piont, prove that
¯¯¯¯¯¯BC.t21+¯¯¯¯¯¯CA.t22+¯¯¯¯¯¯AB.t23=0View SolutionIf tn=14(n+2)(n+3) for n=1,2,3,.... then 1t1+1t2+1t3+....+1t2003=
View Solution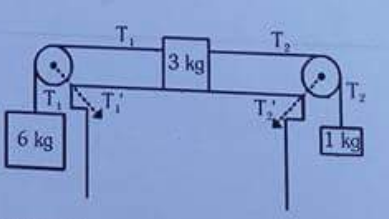
Calculate a, T1,T2,T1'&T2'.View Solutionlimt→124t2−18t3−1
View SolutionProve that the area of the triangle whose vertices are :
(at21,2at1), (at22,2at2), (at23,2at3) is a2(t1−t2)(t2−t3)(t3−t1).View SolutionNormals are drawn to the parabola y2=4ax at the points A, B, C whose parameters are t1,t2andt3, respectively. If these normals enclose a triangle PQR, then prove that its area is a22(t−t2)(t2−t3)(t3−t1)(t1+t2+t3)2 Also prove that ΔPQR=ΔABC(t1+t2+t3)2.
View SolutionA point moving in a straight line with uniform acceleration describes aand b feet in successive intervals of t1 and t2 seconds. Then the acceleration is 2(bt1−at2)t1t2(t1+t2)
Also if the point describes equal distances in successive times t1,t2,t3 then
1t1−1t2+1t3=3t1+t2+t3View Solution

