Two radioactive elements A and B are present in a mixture. Both are beta active. Half lives of A and B are 30 minute and 60 minute respectively. The initial activity of the sample hour only 30 beta particles were detected in an interval of 2 second. Assume that law of radioactivity decay is obeyed.
(a) Find the ratio of number of active of A to that of B in the mixture initially.
(b) The molar mass of both A and B is closed to 200g. The mixture contains other substance (non radioactive) aprt from A and B. what fraction of the entire mixure is radioactive (fraction by weight) if it is given what mass of the mixture is 1μg.
The correct Answer is:(a) 12 (b) 5.2×10−11
Step by step video, text & image solution for Two radioactive elements A and B are present in a mixture. Both are beta active. Half lives of A and B are 30 minute and 60 minute respectively. The initial activity of the sample hour only 30 beta particles were detected in an interval of 2 second. Assume that law of radioactivity decay is obeyed. (a) Find the ratio of number of active of A to that of B in the mixture initially. (b) The molar mass of both A and B is closed to 200g. The mixture contains other substance (non radioactive) aprt from A and B. what fraction of the entire mixure is radioactive (fraction by weight) if it is given what mass of the mixture is 1mug. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
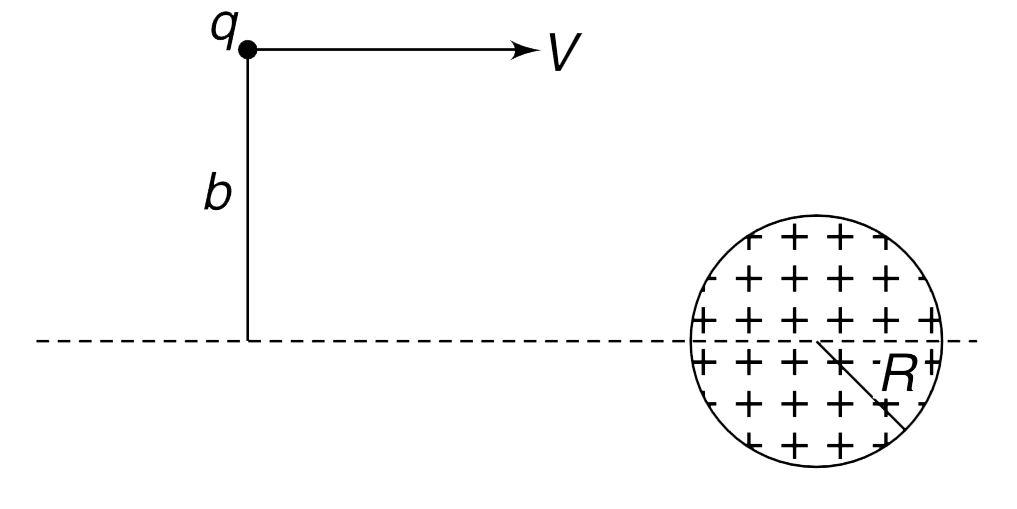
There is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
View SolutionIn the figure shown M represents a mirror. AB is an incident wavefront. Which type of mirror is M if the reflected wave front
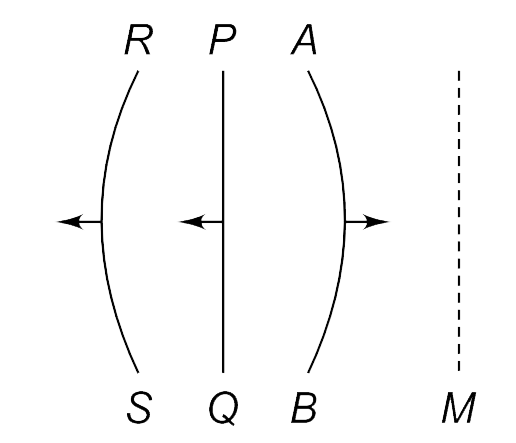
(a)PQ (b)RS
View SolutionHalf-lives of two radioactive elements A and B are 20 minutes and 40 minutes respectively. Initially, the samples have equal number of nuclei. After 80 minutes, the ratio of decayed numbers of A and B nuclei will be
View SolutionA radioactive element A of decay constant lamda_(A) decays into another radioactive element B of decay constant lamda_(B) . Initially the number of active nuclei of A was N_(0) and B was absent in the sample. The maximum number of active nuclei of B is found at t=2. In 2//lamda_(A) . The maximum number of active nuclei of B is
View Solutionदो रेडियोधर्मी तत्व A तथा B की अर्द्ध - आयु क्रमश : 20 मिनट तथा 40 मिनट है । प्रारम्भ में दोनों के नमूनें में नाभिको की सख्या बराबर है। 80 मिनट के उपरांत A तथा B के क्षय नाभिको की संख्या का अनुपात होगा :
View Solutionदो रेडियोधर्मी तत्व A तथा B की अर्द्ध - आयु क्रमश : 20 मिनट तथा 40 मिनट है । प्रारम्भ में दोनों के नमूनें में नाभिको की सख्या बराबर है। 80 मिनट के उपरांत A तथा B के क्षय नाभिको की संख्या का अनुपात होगा :
View Solutionदो रेडियोऐक्टिव तत्व A और B की अर्ध-आयु 20 मिनट और 40 मिनट है। प्रारंभ में दोनों के नमूनों में नाभिकों की संख्या बराबर है। 80 मिनट के उपरांत A और B के क्षय हुए नाभिकों की संख्या का अनुपात होता -
View SolutionHalf lives of two radioactive nuclei A and B are 10 minutes and 20 minutes, respectively. If, initially a sample has equal number of nuclei, then after 60 minutes, the ratio of decayed numbers of nuclei A and B will be:
View SolutionHalf-lives of two radioactive elements A and B are 20 minutes and 40 minutes respectively. Initially, the samples have equal number of nuclei. After 80 minutes, the ratio of decayed numbers of A and B nuclei will be :
View Solutionदो रेडियोधर्मी नाभिको A तथा B की अर्द्धआयु क्रमशः 10 मिनट तथा 20 मिनट है। यदि एक नमूने में आरम्भ में दोनों नाभिको की संख्या बराबर है, तो 60 मिनट पश्चात A तथा B क्षयित नाभिको की संख्या का अनुपात होगा
View SolutionHalf lives of two radioactive elements A and B are 20 minutes and 40 minutes respectively. Initially, the samples have equal number of nuclei. Calculate the ratio of decayed numbers of A and B nuclei after 80 minutes.
View SolutionHalf lives of two radioactive elements A and B are 20 minutes and 40 minutes respectively. Initially, the samples have equal number of nuclei. Calculate the ratio of decayed numbers of A and B nuclei after 80 minutes.
View SolutionHalf lives of two radioactive elements A and B are 20 minutes and 40 minutes respectively. Initially, the samples have equal number of nuclei. Calculate the ratio of decayed numbers of A and B nuclei after 80 minutes.
View SolutionHalf lives of two radioactive nuclei A and B are 10 minutes and 20 minutes respectively, If initially a sample has equal number of nuclei, then after 60 minutes, the ratio of decayed numbers of nuclei A and B will be :
View SolutionTwo radioactive samples consist of equal number of atoms. The half lives are 2 hours and 4 hours respectively. The ratio of their activities then is
View Solution
