Two rings having masses M and 2M respectively, having the same radius are placed coaxially as shown in the figure.
 If the mass distribution on both the rings is non-uniform, then the gravitational potential at point P is
If the mass distribution on both the rings is non-uniform, then the gravitational potential at point P is
−GMR[1√2+2√5]
−GMR[1+22]
zero
cannot be determined from the given information
The correct Answer is:A
As all the points on the periphery of eigher ring are the same distance from point P, the potential at point P due to the whole ring can be calculated as V=−(GM)/(√R2+x2) where x is the axis distance from the centre of the ring. This expression is independent of the fact whether the distribution of mass is uniform or non uniform.
So at P,V=−GM√2R−G×2M√5R=−GMR[1√2+2√5]
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Four rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

View SolutionA rod of length / and of mass M and another rod of length 2/ and mass 2M are arranged as shown below in the figure.The magnitude of gravitational field at point P is
View Solution
Knowledge Check
Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
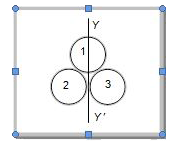 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2A mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
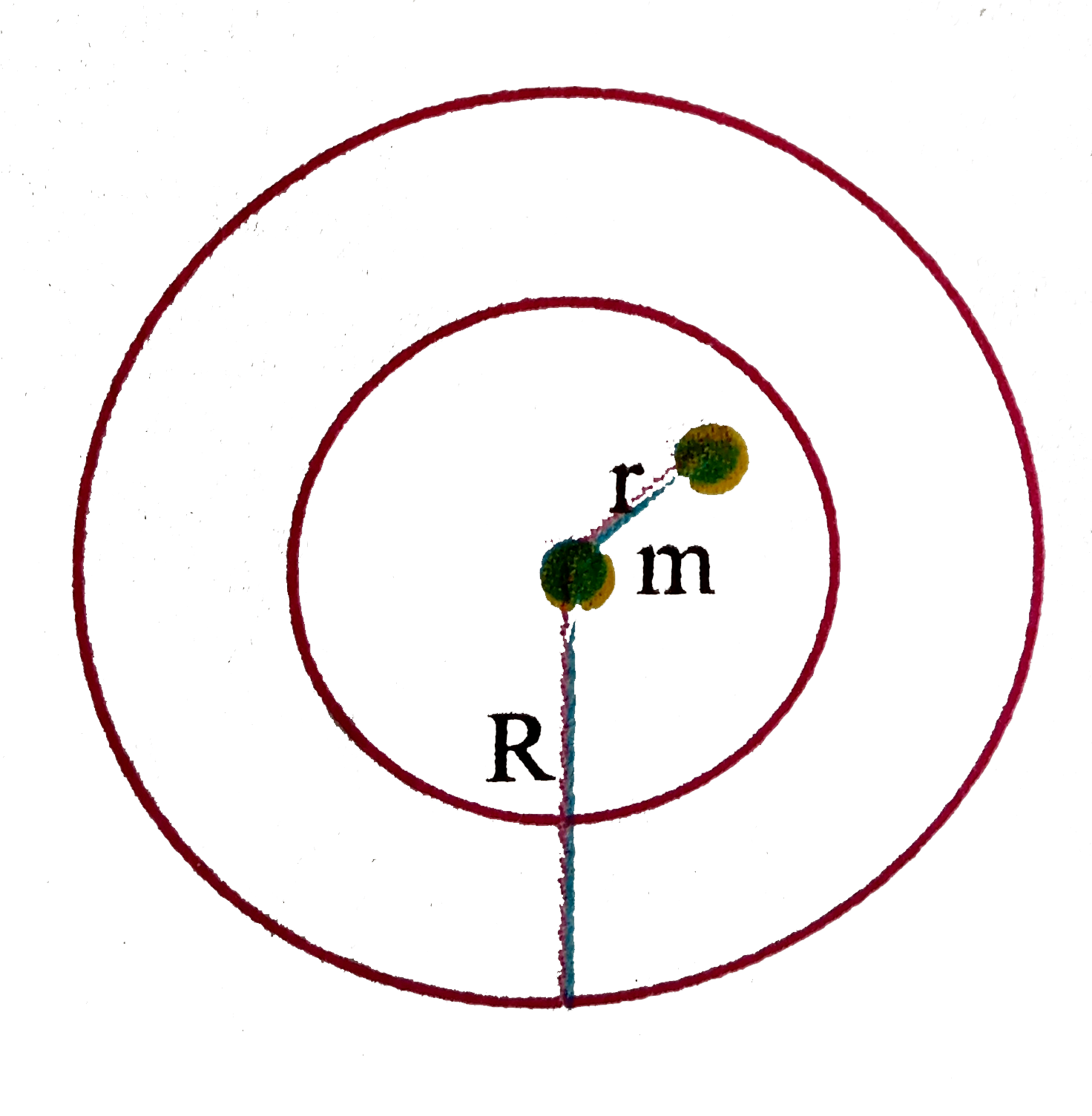 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2DzeroA mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2
A ring of mass M and radius R lies in x−y plane with its centre at origin as shown. The mass distribution of ring is non uniform such that, at any point P on the ring, the mass per unit length is given by λ=λ0cos2θ (where λ0 is a positive constant). Then the moment of inertia of the ring about z-axis is :
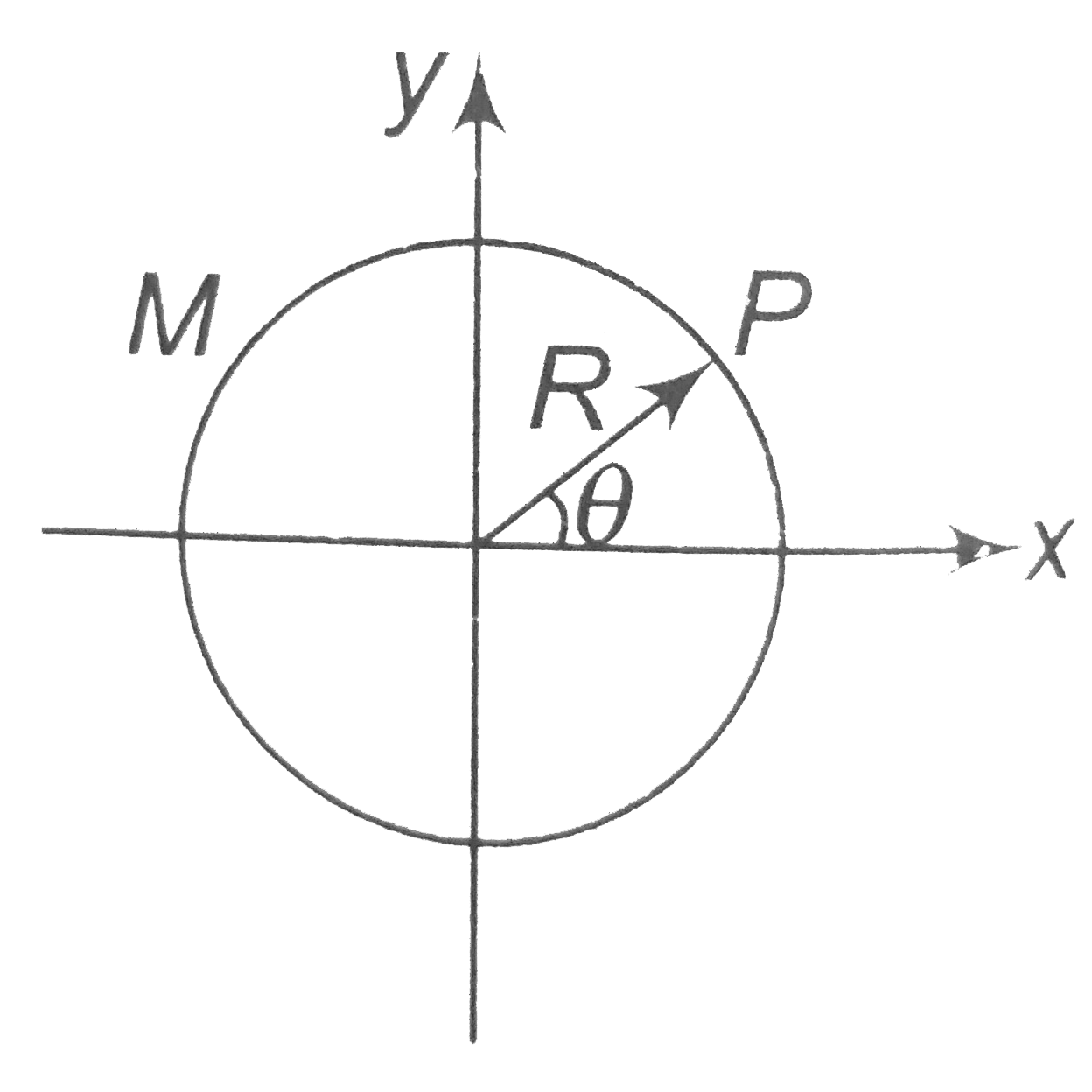 .
.
View SolutionTwo identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
View SolutionFigure (a) shows a ring of mass m and figure (b) shows half portion of the same ring . Gravitational field at point P in figure (b) is I2 in magnitude and makes an angle ϕ with line . AB. Gravitational field at point P in figure (a) is I1 in magnitude . The ratio of I12I2 is
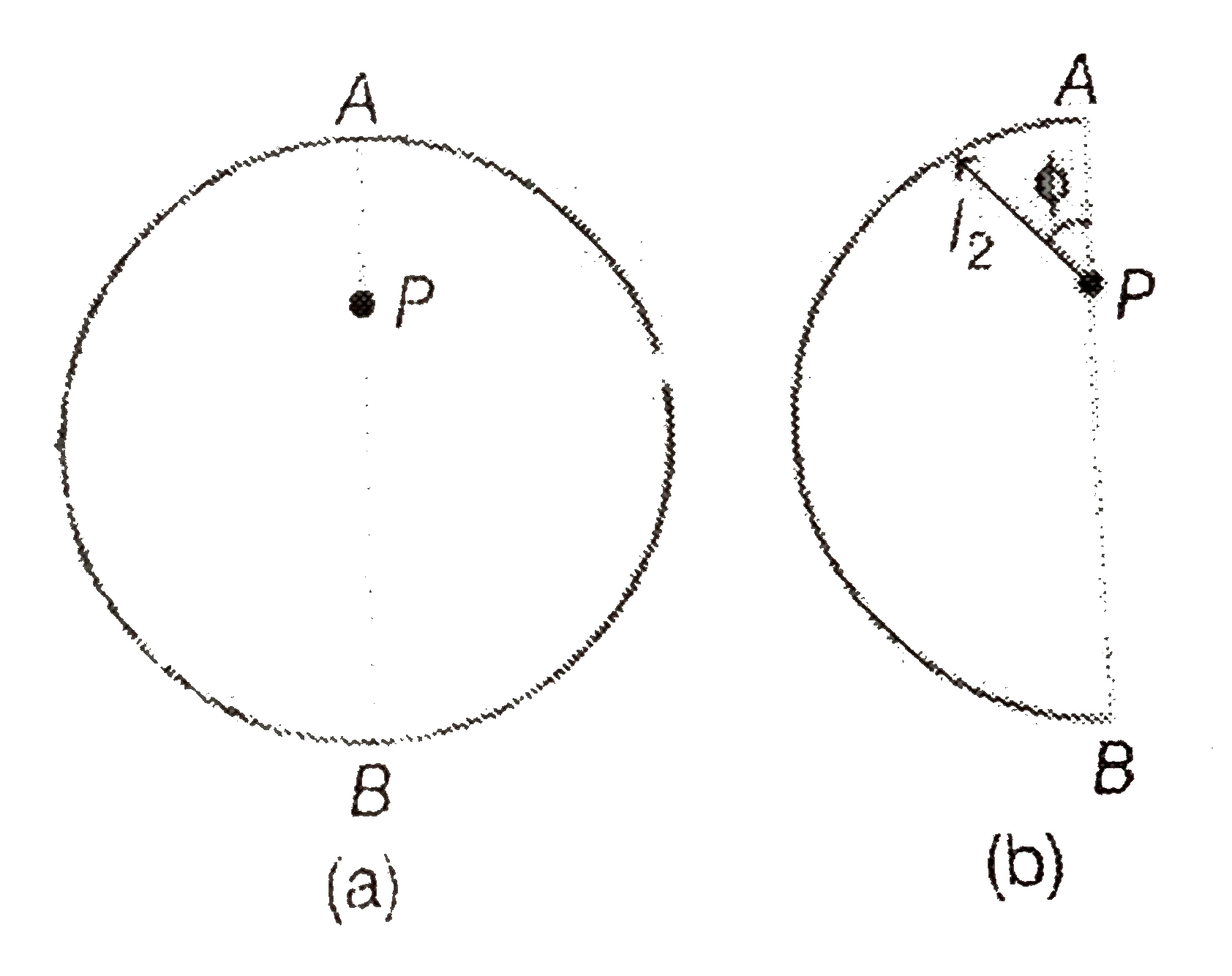
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
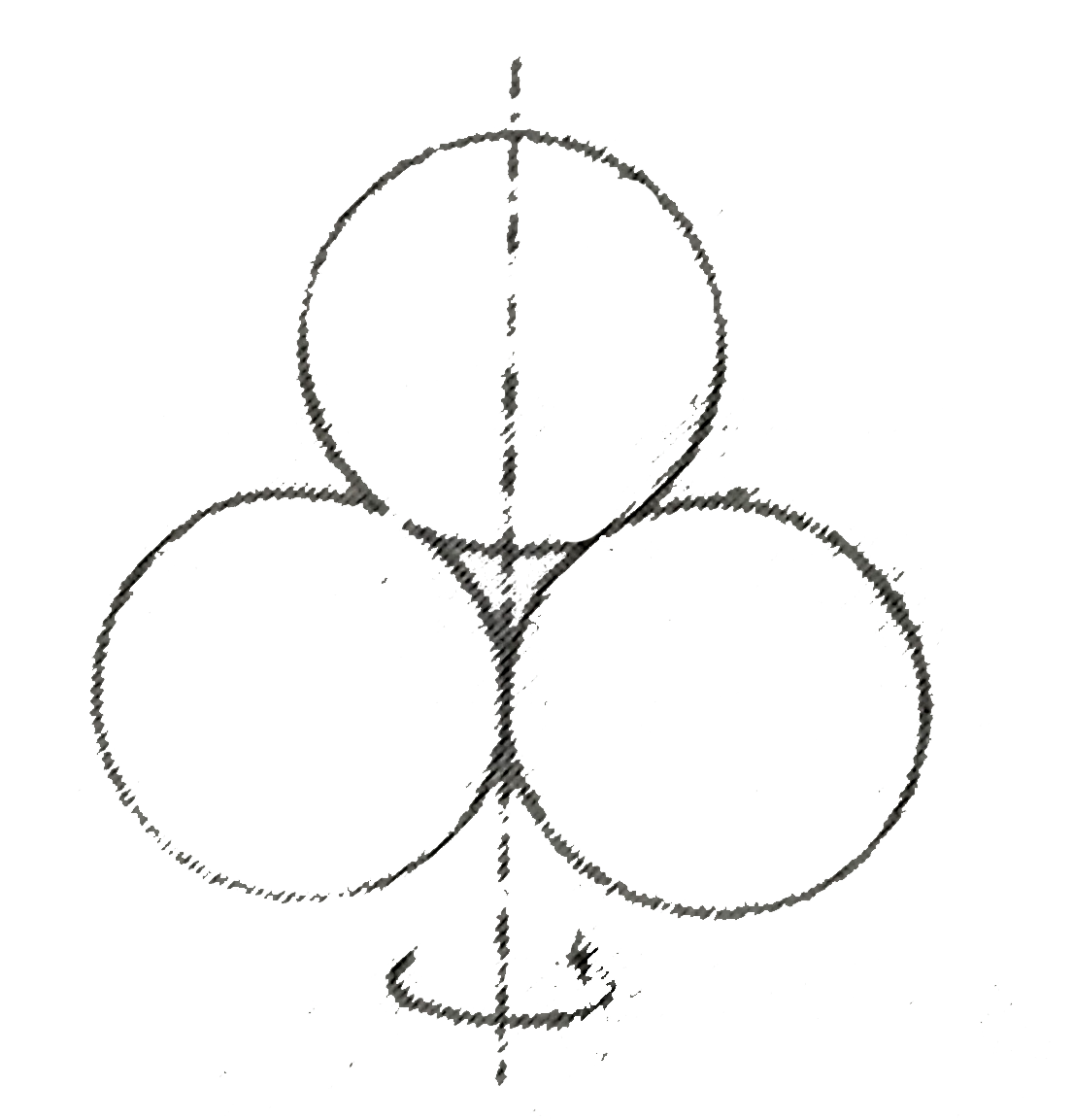
View SolutionA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
View Solution
