Two rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
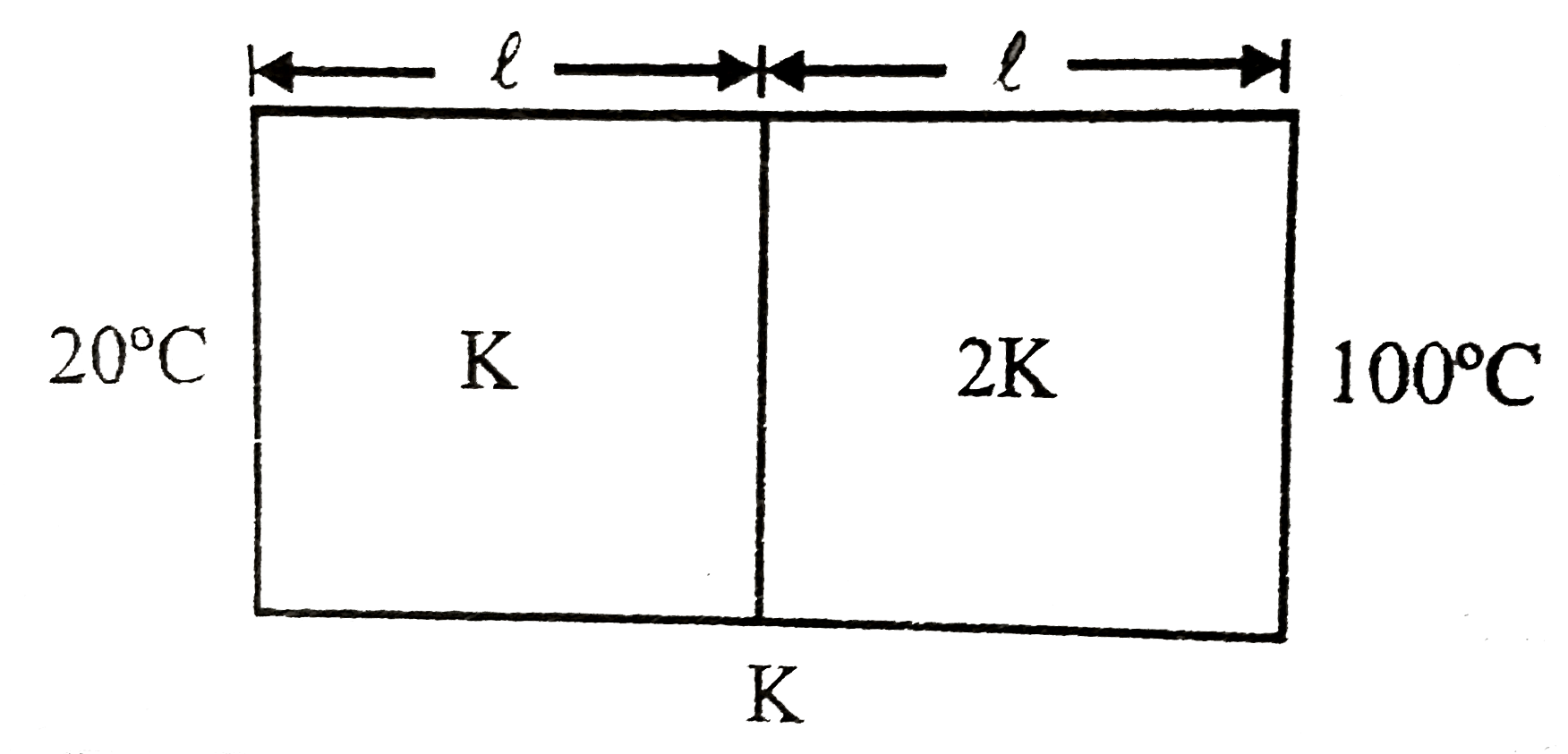
60∘C
73.3∘C
46.7∘C
37.3∘C
The correct Answer is:B
Step by step video & image solution for Two rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (theta) of the interface will be - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEAT TRANSFER & THERMAL EXPANSION BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - EXERCISE - 2
45 Videos
- HEAT TRANSFER & THERMAL EXPANSION BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - Exercise - 3 Section-A
21 Videos
- HEAT TRANSFER & THERMAL EXPANSION BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - SPECIFIC PROBLEMS –
5 Videos
- HEAT - 1BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced
22 Videos
- HEAT-2 BOOK - MOTIONCHAPTER - HEAT-2 EXERCISE - EXERCISE-4 (LEVEL-II)
30 Videos
Similar Questions
Two rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80∘C and the end D is maintained at 10∘C, calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y.

View SolutionIn fig, two bars of the same metal are connected. The length of the first bar is half of that of the second, but the cross-sectional area is double. What is the temperature of the junction of the bars ?

View Solution
Knowledge Check
One end of a metal rod is kept in a furnce. In steady state, the temperature of the rod
AincreasesBdecreasesCremains constantDis non uniform.Seven identical rods of matrical of thermal conductivity k are connected as shown in All the rod are of identical length l and cross sectional area A if the one end b is kept at 100∘C and the other end is kept at 0∘C The temperatures of the junctions C,D and E(θDandθE) be in the steady state
 .AθC>θE>θDBθE=50∘CandθD=37.5∘CCθE=50∘C,θC=62.5∘CandθD=37.5∘CDθE=50∘C,θC=60∘CandθD=40∘C
.AθC>θE>θDBθE=50∘CandθD=37.5∘CCθE=50∘C,θC=62.5∘CandθD=37.5∘CDθE=50∘C,θC=60∘CandθD=40∘C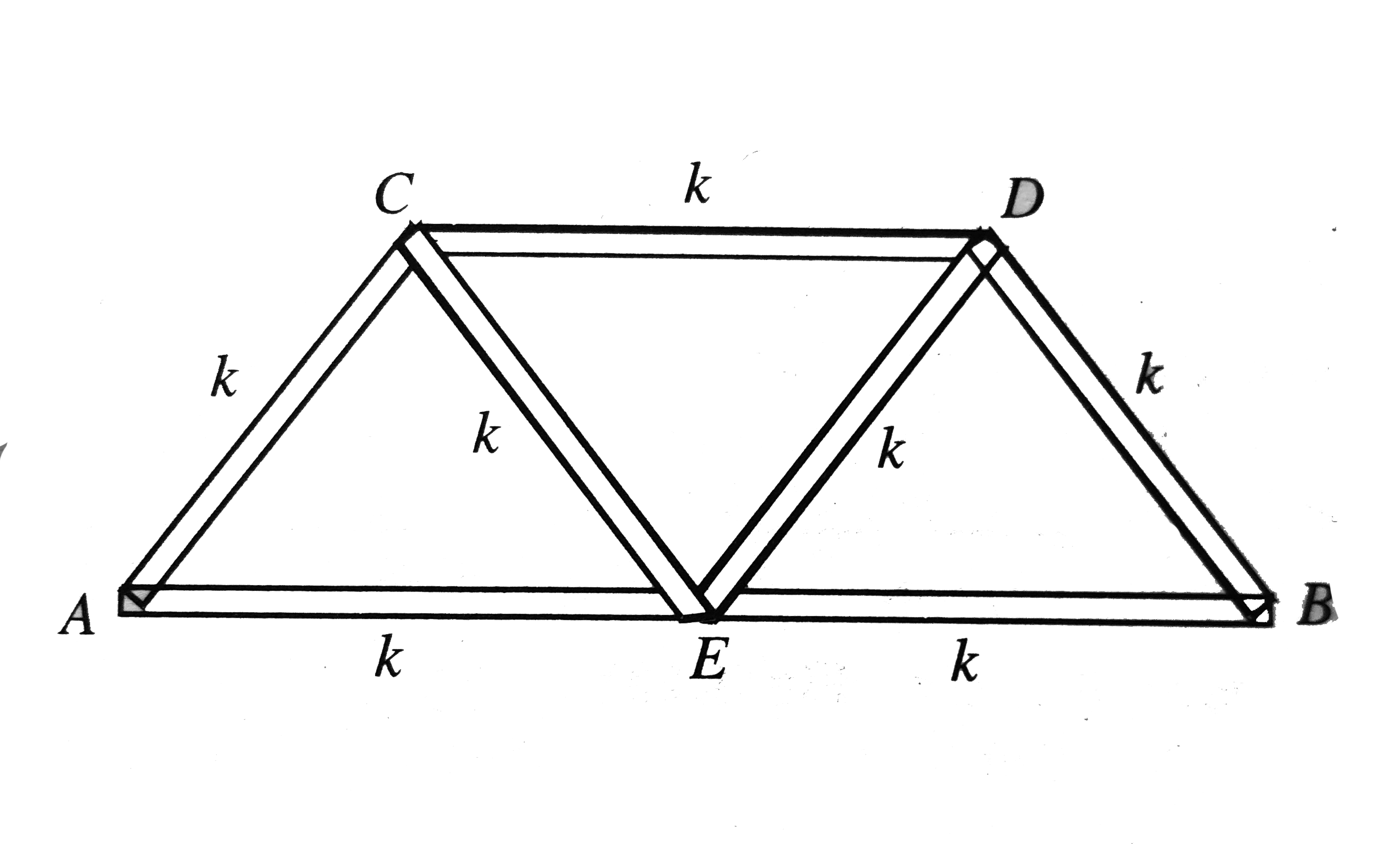
Seven identical rods of material of thermal conductivity k are connected as shown in Fig. All the rods are of identical length l and cross sectional area A If the one end B is kept at 100∘C and the other end is kept at 0∘C what would be the temperatures of the junctions C, D and E(θC,θ)D and θE) in the steady state?AθC>θE>θDBθE=50∘C and θD=37.5∘CCθE=50∘C,θC=62.5∘C and θD=37.5∘CDθE=50∘C,θC=60∘C and θD=40∘C
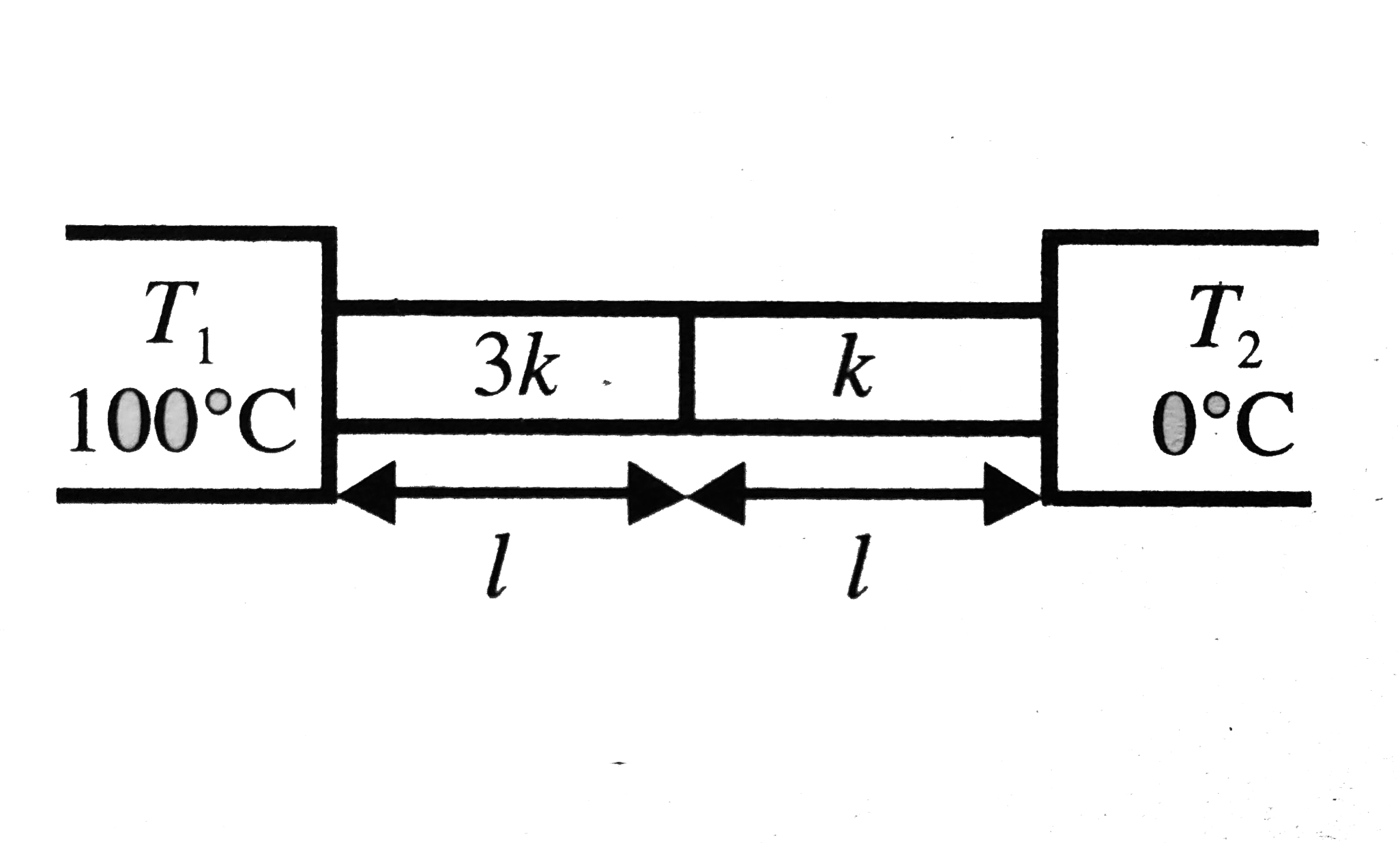
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionTwo metallic rods are connected in series. Both are of same material of same length and same area of cross-section. If the conductivity of each rod be k, then what will be the conductivity of the combination ?
View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
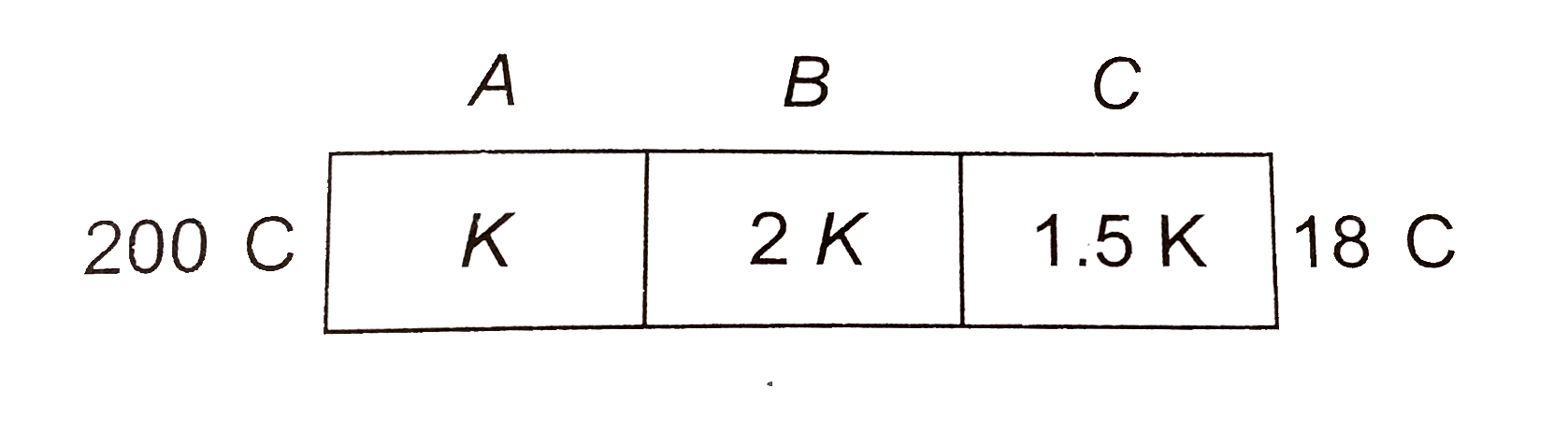
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.

View Solution
