Two satellities 1and2 orbiting with the time periods T1andT2, respectively, lie on the same line as shown in (Fig. 5.167). After what minimum time, again the satellities will remain on the same line ? Assume that the two satellities should lie in same side of the center of their concentric circular paths.
 .
.
Let the satellities 1and2 describe angles θ1andθ2 at the center of earth during a time t, respectively. Suppose 2 is ahead of by 1 by an angle θ. Hence, we can write
θ=θ2−θ1
They will be again lie on same line after a minimum time T' sat. For this θ=2π. This gives θ2−θ1=2π. Dividing T' in both sides,
we have θ2T'−θ1T'=2πT'
Substituting θ2T'=ω2andθ1T'=ω1, we have
2πT'=ω2−ω1 where ω2=2πT2 and ω1=2πT1.
Then, 1T'=1T2−1T1
This gives T'=T1T2T1−T2

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective40videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct76videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.312videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
Find the value of t for which the points (1,-1),(3,-3) and (t,2) lie on the same line (using determinants).
View SolutionTwo bodies having masses 10kg and 5kg are moving in concentric orbits of radii 4 and 8 such that their time periods are the same. Then the ratio of their centripetal accelerations is
View Solution
Knowledge Check
- Question 1 - Select One
A machine part is diagrammed in the figure below with the dimensions given in inches. If the centers of the circles lie on the same line parallel to the bottom of the part, what is the distance, in inches, between the centers of the 2 holes in the machine part?
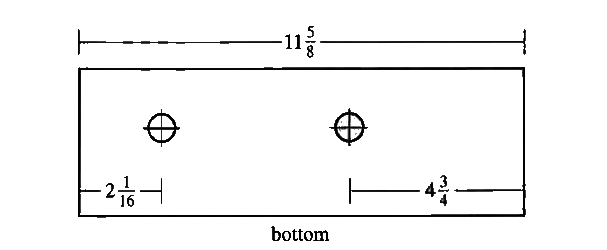 A5316B5116C5D41316
A5316B5116C5D41316 - Question 2 - Select One
Two particles of equal masses are revolving in circular paths of radii, r1andr2 respectively with the same period . The ratio of their centripetal force is -
Ar1/r2B√r2/r1C(r1/r2)2D(r2/r1)2
Two pendulums X and Y of time periods 4s and 4.2s are made to vibrate simultaneously. They are initially in same phase. After how many vibration of X, they will be in the same phase again ?
View SolutionTwo radioactive samples of different elements (half-lives t1 and t2 respectively) have same number of nuclei at t=0. The time after which their activities are same is
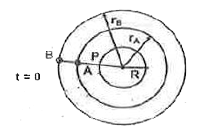
View SolutionTwo satellite A and B are travelling in the same plane and same sense in circular orbit around the earth at an atitude rA and rB from the centre of the earth respectively. If at time t=0 the satellite are aligned as shown in the figure, knowing that the radius of the earth R. Determine the time at which again the satellite will be aligned as they were at t=0
 View Solution
View SolutionA mass is suspended separately by two different springs in successive order then time period is t1 and t2 respectively. If it is connected by both spring as shown in figure then time period is t0, the correct relation is : -
 View Solution
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionIf the radii of circular path of two particles are in the ratio of 1:2, then in order to have same centripetal acceleration, their speeds should be in the ratio of :
View Solution

