Two sinusoidal waves y1,(x,t)andy2(x,t) have the same wavelength and travel together in the same direction along a string. Their amplitudes are ym1= 4.0 mm and ym2=3.0mm, and their phase constants are 0 and π/3 rad, respectively. What are the amplitude ym', and phase constant of the resultant wave? Write the resultant wave in the form of Eq. 16-63.
(1) The two waves have a number of properties in commom: Because they travel along the same string, they must have the same speed v as set by the tension and incar density of the string according to Eq: 16.29 With the name wavelength, λ they have the same angular wave numbe k(=2π/λ). Also, because they have the same wave number k and speed y, they must have the same angular frequency ω(=kv).
(2) The waves (call them waves 1 and 2) can be represented by phasors rotating at the same angular speed ω about an origin. Because the phase constant for wave ω is greater than that for wave 2 is greater than that for wave 1 by π/3, phasor 2 must lag phasor 1 by π/3 rad in their clockwise rotation, as shown in Fig. 16-24a. The resultant wave due to the interference of waves 1 and 2 can then be represented by a phasor that is the vector sum of phasors 1 and 2.
Calculations : To simplify the vector summation, we drew phasors 1 and 2 in Fig 16-24 a at the instant when phasor 1 lies along the horizontal axis. We then drew laging phasor 2 at positive angle π/3 rad. In Fig 16-24b we shifted phasor 2 so tail is at the 1. Then
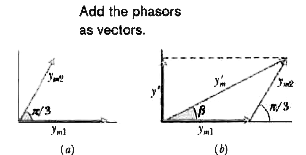
we can draw the phasor ym. of the resultant wave from the tail of phasor 1 to the head of phasor 2. The phase constant B is the angle phasor ym. makes with phasor 1.
To find values for ym.andβ, we can sum phasors 1 and 2 as vectors on a vector-capable calculator. However, here we shall sum them by components. (They are called horizontal and vertical components, because the symbols x and y are already used for the waves themselves.) For the horizontal components we have
ymh.=ym1cos0+ym2cosπ/3
=4.0mm+(3.0mm)cosπ/3)=5.50mm
For the vertical components we have
ymv.=ym1cos0+ym/2sinπ/3
=0+(3.0mm)sinπ/3=2.60mm,
Thus, the resultant wave has an amplitude of
ym.=√(5.50mm)2+(2.60mm)2
=6.1 mm
and a phase constant of bet=tan−1(2.60mm)5.50mm=0.44rad
From Fig. 16-24b, phase constant β is a positive angle relative to phasor 1. Thus, the resultant wave lags wave 1 in their travel by phase constant β=+0.44 rad. From Eq. 16 -63, we can write the resultant wave y.(x,t)=(6.1mm)sin(kx−ωt+0.44rad).
Topper's Solved these Questions
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Checkpoint
Explore 8 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Problems
Explore 60 Videos
- WAVE - IIBook:RESNICK AND HALLIDAYChapter:WAVE - IIExercise:PRACTICE QUESTIONS (INTEGER TYPE)
Explore 5 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
Similar Questions
Two waves of amplitudes 3mmand2mm reach a point in the same phase. What is the resultant amplitude ?
View SolutionTwo sinusoidal wave having the same frequency and travelling in the same direction are combined. What is the amplitude of the resultant motion if their amplitudes are 3cm and 4cm and they differ in phase by π/2 radian?
View Solution
Knowledge Check
Two identical sinusoidal waves each of amplitude 5 mm with a phase difference of π/2 are traveling in the same direction in a string. The amplitude of the resultant wave (in mm) is
AzeroB5√2C5√2D2.5Two identical sinusoidal waves each of amplitude 10 mm with a phase difference of 90∘ are travelling in the same direction in a string. The amplitude of the resultant wave is
A5 mmB10√2 mmC15 mmD20 mmTwo identical sinusoidal waves each of amplitude 10 mm with a phase difference of 90∘ are travelling in the same direction in a string. The amplitude of the resultant wave is
A5 mmB10√2 mmC15 mmD20 mm
Two sinusoidal waves of the same frequency travel in the same direction along a string. If ym1=2.0cm,ym2=4.0cm,ϕ1=0,andϕ2=π/2rad, what is the amplitude of the resultant wave?
View SolutionTwo sinusoidal waves of the same frequency travel in the same direction along a string. If A1=m3.0cm,A2=4.0cm,ϕ1=0, and ϕ2=π/2rad, what is the amplitude of the resultant wave ?
View SolutionTwo sinusoidal waves of the same frequency travel in the same direction along a string. If A1=m3.0cm,A2=4.0cm,ϕ1=0, and ϕ2=π/2rad, what is the amplitude of the resultant wave ?
View SolutionThree sinusodal waves having amplitudes a, a/2 and a/3 are superposed. They have the same period and thelr phase are 0, π/2 and respectively. Find (i) The resultant amplitude and phase (ii) Draw a sketch to show the resultant wave.
View SolutionThree component sinusoidal waves progressing in the same directions along the same path have the same period byt their amplitudes are A,A2andA3. The phases of the variation at any position x on their path at time t=0are0,−π2and−π respectively. Find the amplitude and phase of the resultant wave.
View Solution
