Two slabs A and B of equal surface area are placed one over the other such that their surfaces are completely in contact. The thickness of slab A is twice that of B. The coefficient of thermal conductivity of slab B is maintained at 25∘C. The temperature at the contact of their surface is
62.5∘C
45∘C
55∘C
85∘C
To solve the problem, we need to determine the temperature at the contact surface of the two slabs A and B. Here's a step-by-step breakdown of the solution:
Step 1: Define the parameters
- Let the thickness of slab B be L.
- Therefore, the thickness of slab A, which is twice that of slab B, will be 2L.
- Let the coefficient of thermal conductivity of slab B be K. Thus, the coefficient of thermal conductivity of slab A will be 2K.
- The temperature at the surface of slab A is maintained at 100∘C, and the temperature at the surface of slab B is maintained at 25∘C.
Step 2: Write the heat flow equations
Since the slabs are in series, the rate of heat flow through both slabs must be equal. The heat flow Q through a slab can be expressed using Fourier's law of heat conduction:
For slab A:
Q=KA⋅A⋅(T1−T)dA
Where:
- KA=2K (thermal conductivity of slab A)
- A is the area
- T1=100∘C (temperature at the surface of slab A)
- T is the temperature at the contact surface
- dA=2L (thickness of slab A)
So, the equation becomes:
Q=2K⋅A⋅(100−T)2L
This simplifies to:
Q=K⋅A⋅(100−T)L(1)
For slab B:
Q=KB⋅A⋅(T−T2)dB
Where:
- KB=K (thermal conductivity of slab B)
- T2=25∘C (temperature at the surface of slab B)
- dB=L (thickness of slab B)
So, the equation becomes:
Q=K⋅A⋅(T−25)L(2)
Step 3: Set the heat flow equations equal
Since the heat flow through both slabs is the same, we can set equations (1) and (2) equal to each other:
K⋅A⋅(100−T)L=K⋅A⋅(T−25)L
Step 4: Simplify the equation
We can cancel K and A from both sides (assuming they are not zero):
100−T=T−25
Step 5: Solve for T
Now, rearranging the equation gives:
100+25=2T
125=2T
T=1252=62.5∘C
Conclusion
The temperature at the contact of the surfaces of slabs A and B is 62.5∘C.
---
- Let the thickness of slab B be L.
- Therefore, the thickness of slab A, which is twice that of slab B, will be 2L.
- Let the coefficient of thermal conductivity of slab B be K. Thus, the coefficient of thermal conductivity of slab A will be 2K.
- The temperature at the surface of slab A is maintained at 100∘C, and the temperature at the surface of slab B is maintained at 25∘C.
Since the slabs are in series, the rate of heat flow through both slabs must be equal. The heat flow Q through a slab can be expressed using Fourier's law of heat conduction:
Q=KA⋅A⋅(T1−T)dA
Where:
- KA=2K (thermal conductivity of slab A)
- A is the area
- T1=100∘C (temperature at the surface of slab A)
- T is the temperature at the contact surface
- dA=2L (thickness of slab A)
Q=2K⋅A⋅(100−T)2L
This simplifies to:
Q=K⋅A⋅(100−T)L(1)
Q=KB⋅A⋅(T−T2)dB
Where:
- KB=K (thermal conductivity of slab B)
- T2=25∘C (temperature at the surface of slab B)
- dB=L (thickness of slab B)
Q=K⋅A⋅(T−25)L(2)
Since the heat flow through both slabs is the same, we can set equations (1) and (2) equal to each other:
K⋅A⋅(100−T)L=K⋅A⋅(T−25)L
We can cancel K and A from both sides (assuming they are not zero):
100−T=T−25
Now, rearranging the equation gives:
100+25=2T
125=2T
T=1252=62.5∘C
The temperature at the contact of the surfaces of slabs A and B is 62.5∘C.
Topper's Solved these Questions
Similar Questions
Two plates of equal areas are placed in contact wih each other. Their thickness are 2.0 cm and 5.0 cm respectively. The temperature of the external surface of the first plate is −20∘C and that of the external surface of the second plate is 20∘C. What will be the temperature of the current surface if the plates (i) are of the same material, (ii) have thermal conductivities in the ratio 2:5.
View SolutionThere are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
View Solution
Knowledge Check
Two slabs A and B of equal surface area are placed one over the other such that their surfaces are completely in contact The thickness and coefficient of thermal conductivities of slab A is twice that B The first surface of slab A is maintained at 100∘C while the second surface of slab B is maintained at 25∘C The temperature at the contact of their surfaces is .
A15∘CB62.5∘CC55∘CD85∘CTwo plates of same area are placed in contact. Their thickness as well as thermal conductivities are in the ratio 2:3. The outer surface of one plate is maintained at 10∘C and that of the other at 0∘C. What is the temperature at the common surface?
A0∘CB2.5∘CC5∘CD6.5∘CTwo plates of equal areas are placed in contact with each other . Their thickness are 2cm and 3cm respectively. Temperature of the external surface of the first plate is −25∘C and that of the external surface of the second plate is 25∘C What will be temperature of contact surface if the plates:-
(i) Are of same material (ii) Have thermal conductivity in ratio 2:3.A(i)−5∘C (ii) 0∘CB(i) 5∘C (ii)0∘CC(i) 0∘C (ii) −5∘CDNone of these
A and B are two cones. The curved surface area of A is twice that of B. The slant height of B is twice that of A. Whatis the ratio of radii of A to B?
View SolutionThere are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. The ratio of their radii is
View SolutionTwo blocks A and B are placed one over the other on a smooth horizontal surface. The maximum horizontal force that can be applied on the lower block A, so that A and B move without separation is 49N. The coefficient of friction between A and B is (take g = 9.8ms−2 )
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View Solution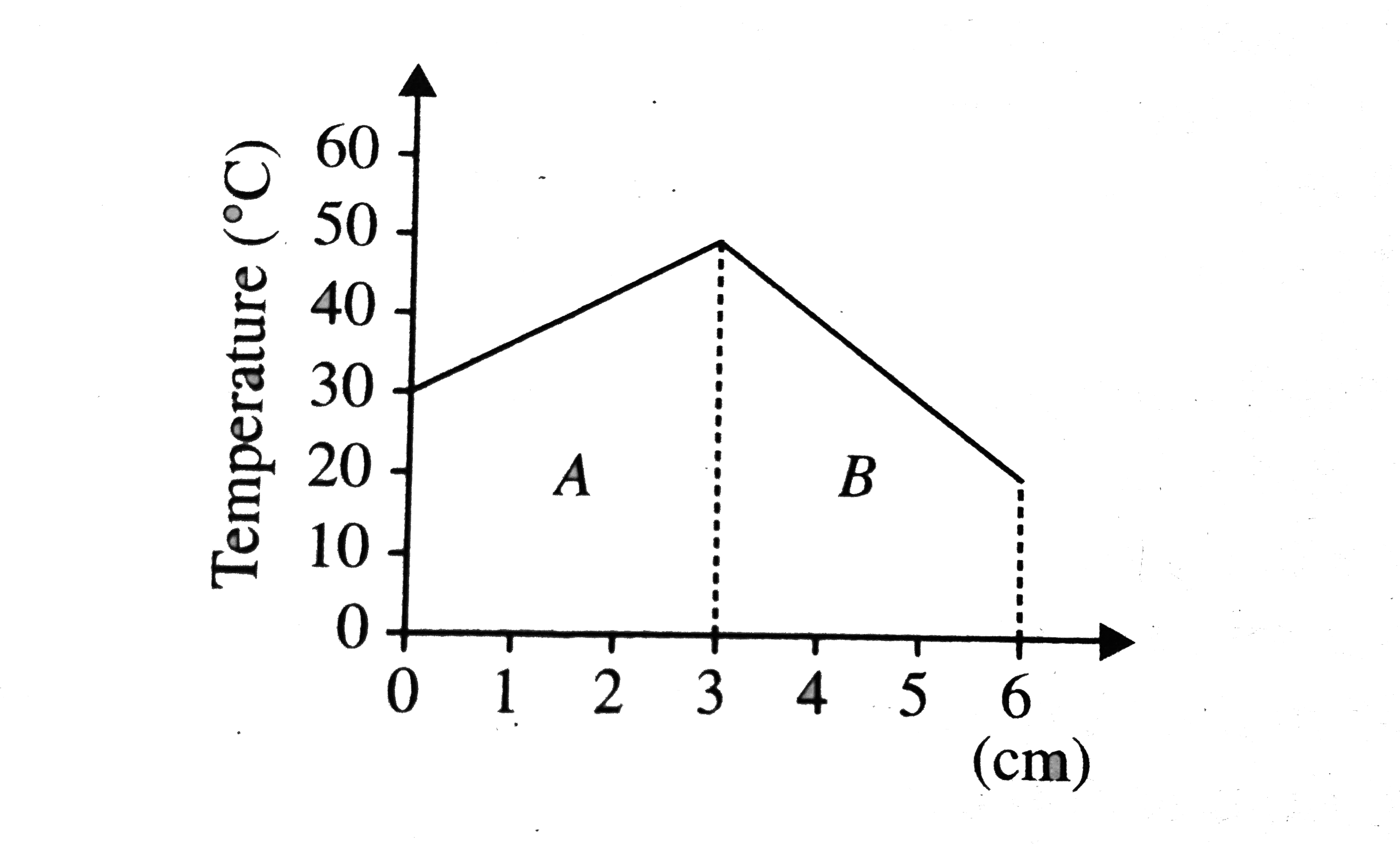
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is
View Solution
