Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
√2K
3K
43K
23K
The correct Answer is:C
To find the equivalent thermal conductivity of a compound slab consisting of two different materials with equal thickness and thermal conductivities K and 2K, we can follow these steps:
Step 1: Understand the Setup
We have a compound slab made of two materials:
- Material 1 has thermal conductivity K and thickness L.
- Material 2 has thermal conductivity 2K and thickness L.
Step 2: Calculate the Thermal Resistance
The thermal resistance R for each material can be calculated using the formula:
R=LkA
where:
- L is the thickness of the material,
- k is the thermal conductivity,
- A is the cross-sectional area.
For Material 1 (conductivity K):
R1=LKA
For Material 2 (conductivity 2K):
R2=L2KA
Step 3: Combine the Resistances
Since the two materials are in series, the total thermal resistance Rtotal of the slab is the sum of the individual resistances:
Rtotal=R1+R2=LKA+L2KA
Step 4: Simplify the Expression
To combine the resistances, we can find a common denominator:
Rtotal=LKA+L2KA=2L2KA+L2KA=2L+L2KA=3L2KA
Step 5: Calculate the Equivalent Thermal Conductivity
The equivalent thermal conductivity Keq can be defined using the total resistance:
Rtotal=LKeqA
Setting the two expressions for Rtotal equal to each other:
LKeqA=3L2KA
Step 6: Solve for Keq
By cross-multiplying and simplifying, we can solve for Keq:
Keq=2K3
Final Answer
The equivalent thermal conductivity of the compound slab is:
Keq=2K3
---
We have a compound slab made of two materials:
- Material 1 has thermal conductivity K and thickness L.
- Material 2 has thermal conductivity 2K and thickness L.
The thermal resistance R for each material can be calculated using the formula:
R=LkA
where:
- L is the thickness of the material,
- k is the thermal conductivity,
- A is the cross-sectional area.
R1=LKA
R2=L2KA
Since the two materials are in series, the total thermal resistance Rtotal of the slab is the sum of the individual resistances:
Rtotal=R1+R2=LKA+L2KA
To combine the resistances, we can find a common denominator:
Rtotal=LKA+L2KA=2L2KA+L2KA=2L+L2KA=3L2KA
The equivalent thermal conductivity Keq can be defined using the total resistance:
Rtotal=LKeqA
Setting the two expressions for Rtotal equal to each other:
LKeqA=3L2KA
By cross-multiplying and simplifying, we can solve for Keq:
Keq=2K3
The equivalent thermal conductivity of the compound slab is:
Keq=2K3
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - AIIMS Questions
28 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion Reasoning
21 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test
28 Videos
Similar Questions
Two identical metal wires of thermal conductivities K1 and K2 respectively are connected in series. The effective thermal conductivity of the combination is :
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
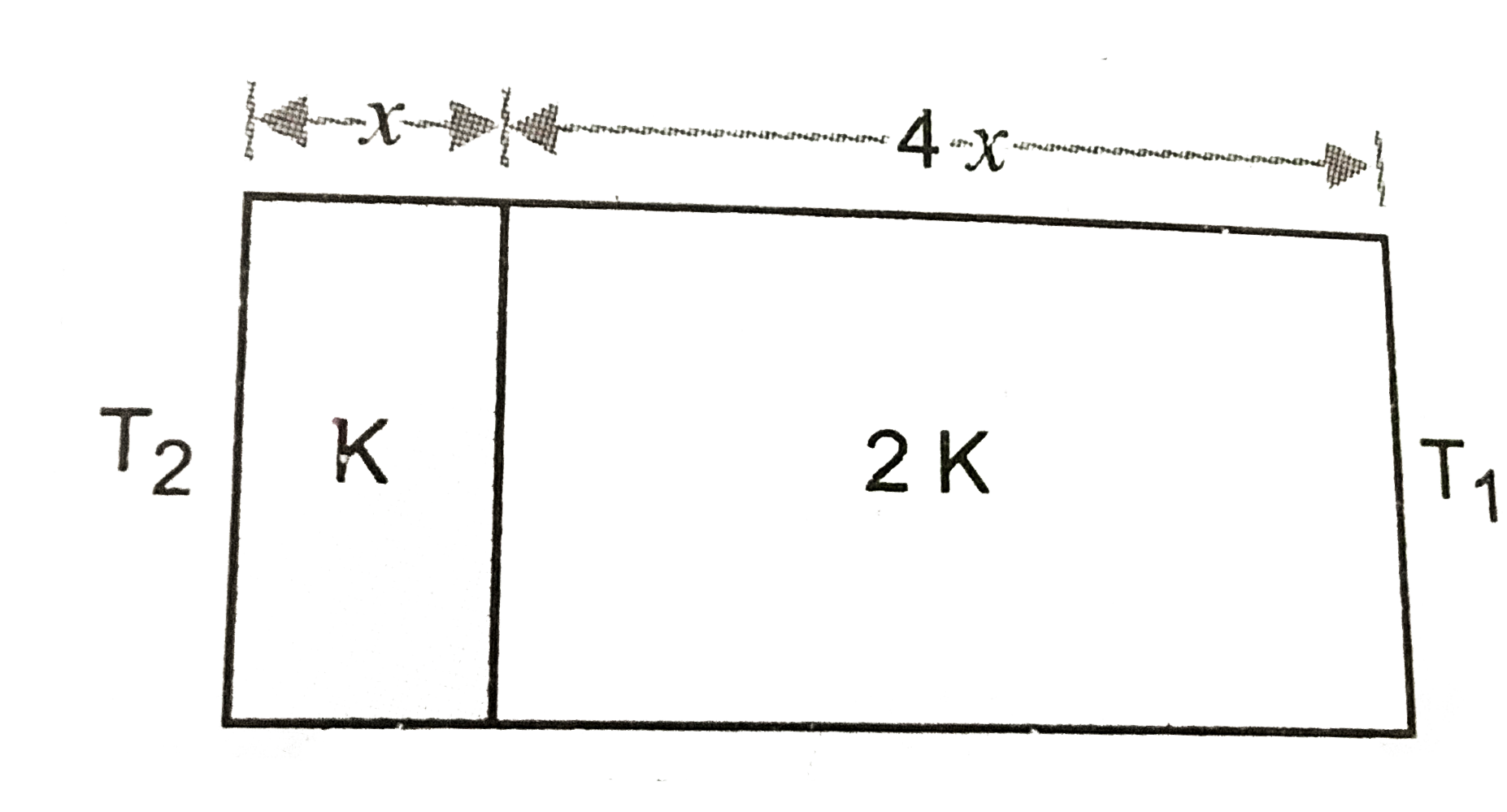
View Solution
Knowledge Check
Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
A√2B3 KC43KD23KA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
AK1+K2BK1K2K1+K2C√K1K2D2K1K2K1+K2A slab consists of two parallel layers of two different materials of same thickness having thermal conductivities K1andK2. The equivalent conductivity of the combination is
AK1+K2BK1+K22C2K1K2K1+K2DK1+K22K1K2
Two rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionTwo rods of the same length and diameter, having thermal conductivities K1 and K2, are joined in parallel. The equivalent thermal conductivity to the combinationk is
View SolutionTwo rods of equal length and diameter but of thermal conductivities 2 and 3 unites respectively are joined in parallel. The thermal conductivity of the combination is:
View SolutionIn the question number of 45, the equivalent thermal conductivity of the compound bar is
View Solution
