Two soap bubbles, one of radius 50mm and the other of radius 80mm, are brought in contact so that they have a common interface. The radius of the curvature of the common interface is
0.003m
0.133m
1.2m
8.9m
The correct Answer is:B
To find the radius of curvature of the common interface between two soap bubbles, we can use the formula derived from the principles of fluid mechanics. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have two soap bubbles with radii R1=50mm and R2=80mm that are in contact with each other. We need to find the radius of curvature R of the common interface.
Step 2: Use the Formula for Radius of Curvature
The formula for the radius of curvature R of the common interface between two soap bubbles is given by:
1R=1R1+1R2
This formula arises from the balance of pressures inside the bubbles.
Step 3: Substitute the Values
Substituting the values of R1 and R2 into the formula:
1R=150+180
Step 4: Find a Common Denominator
To add the fractions, we need a common denominator. The least common multiple of 50 and 80 is 400. Thus, we rewrite the fractions:
150=8400,180=5400
Step 5: Add the Fractions
Now we can add the fractions:
1R=8400+5400=13400
Step 6: Invert to Find R
To find R, we take the reciprocal of both sides:
R=40013mm
Step 7: Calculate the Value
Now, we can calculate the value:
R≈30.77mm
Conclusion
The radius of curvature of the common interface is approximately 30.77mm.
---
We have two soap bubbles with radii R1=50mm and R2=80mm that are in contact with each other. We need to find the radius of curvature R of the common interface.
The formula for the radius of curvature R of the common interface between two soap bubbles is given by:
Substituting the values of R1 and R2 into the formula:
To add the fractions, we need a common denominator. The least common multiple of 50 and 80 is 400. Thus, we rewrite the fractions:
Now we can add the fractions:
To find R, we take the reciprocal of both sides:
Now, we can calculate the value:
The radius of curvature of the common interface is approximately 30.77mm.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct
17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective
16 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A soap bubble A of radius 0.03 m and another bubble B of radius 0.04 m are brought together, so that the combined bubble has a common interface of radius r, then the value of r is
View SolutionTwo soap bubbles one of radius 3cm and other of radius 4cm each coaless in vacuum under isothermal conditons. Calculate the radius of the bubble formed ?
View Solution
Knowledge Check
Two metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
A52σ,54σB53σ,56σC35σ,65σD23σ,12σ
Two soap bubbles of radii 2 cm and 3 cm are brought in contact. Find the radius of curvature (in cm) of the contact surface.
View SolutionTwo soap bubbles with radius 2r and 3r come in contact. Their common surface has a radius of curvature nr, then find the value of n
View SolutionTwo soap bubbles with radii of curvature R1andR2 where R2<R1 are brought into contact as shown in Fig. 21.10. What is the radius of curvature of the film between them? What is the contact angle of the films?

View SolutionA soap bubble of radius r is placed on another bubble of radius 2r. The radius of the surface common to both the bubbles is
View SolutionTwo metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
View SolutionTwo soap bubbles of radii r1 and r2 equal to 4 cm and 5 cm are touching each other over a common surface S1S2 (shown in figure). Its radius will be
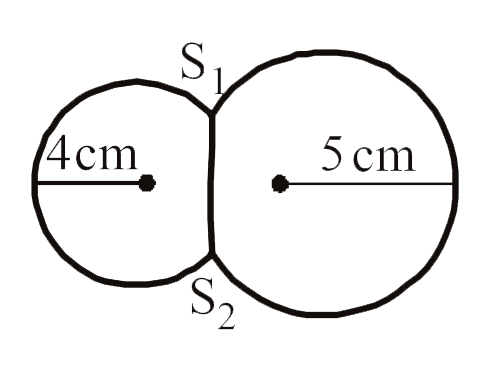
View SolutionA plano-convex lens P and a concavo-convex lens Q are in contact as shown in figure. The refractive index o fthe material of the lens P and Q is 1.8and1.2 respectively. The radius of curvature of the concave surface of the lens Q is double the radius of curvature of the convex surface. The convex surface of Q is silvered.

The radius of curvature of common surface is
View Solution
