The velocity of small ball of mass M and density (d1= when dropped a container filled with glycerine becomes constant after some time. If the density glycerine is d2, the viscous force acting on ball is
Md1gd2
Mg(1−d2d1)
M(d1+d2)g
Md1d2
The correct Answer is:B
To find the viscous force acting on a small ball of mass M and density d1 when it is dropped in a container filled with glycerine of density d2, we can follow these steps:
1. Understanding Terminal Velocity:
- When the ball is dropped in glycerine, it eventually reaches a constant velocity known as terminal velocity. At this point, the net force acting on the ball is zero.
2. Forces Acting on the Ball:
- The forces acting on the ball are:
- The weight of the ball, W=Mg, where g is the acceleration due to gravity.
- The buoyant force (upthrust) acting on the ball, which is equal to the weight of the liquid displaced by the ball.
3. Calculating the Buoyant Force:
- The volume of the ball can be expressed as V=43πR3 (where R is the radius of the ball).
- The mass of the liquid displaced by the ball is given by mass of liquid=d2×V.
- Therefore, the buoyant force Fb is:
Fb=mass of liquid×g=d2×V×g=d2×(43πR3)g
4. Applying the Equilibrium Condition:
- At terminal velocity, the viscous force Fv plus the buoyant force Fb balances the weight of the ball:
Fv+Fb=W
- Rearranging gives us the expression for the viscous force:
Fv=W−Fb
5. Substituting the Values:
- Substitute W=Mg and Fb=d2×V×g:
Fv=Mg−d2(43πR3)g
6. Expressing the Volume in Terms of Density:
- The volume V of the ball can also be expressed in terms of its mass and density:
V=Md1
- Substitute this into the expression for the buoyant force:
Fb=d2(Md1)g
7. Final Expression for Viscous Force:
- Now substituting Fb back into the equation for Fv:
Fv=Mg−d2(Md1)g
- Factor out g:
Fv=g(M−d2Md1)
- Simplifying gives:
Fv=Mg(1−d2d1)
8. Final Result:
- Thus, the viscous force acting on the ball is:
Fv=Mg(d1−d2)d1
- When the ball is dropped in glycerine, it eventually reaches a constant velocity known as terminal velocity. At this point, the net force acting on the ball is zero.
- The forces acting on the ball are:
- The weight of the ball, W=Mg, where g is the acceleration due to gravity.
- The buoyant force (upthrust) acting on the ball, which is equal to the weight of the liquid displaced by the ball.
- The volume of the ball can be expressed as V=43πR3 (where R is the radius of the ball).
- The mass of the liquid displaced by the ball is given by mass of liquid=d2×V.
- Therefore, the buoyant force Fb is:
Fb=mass of liquid×g=d2×V×g=d2×(43πR3)g
- At terminal velocity, the viscous force Fv plus the buoyant force Fb balances the weight of the ball:
Fv+Fb=W
- Rearranging gives us the expression for the viscous force:
Fv=W−Fb
- Substitute W=Mg and Fb=d2×V×g:
Fv=Mg−d2(43πR3)g
- The volume V of the ball can also be expressed in terms of its mass and density:
V=Md1
- Substitute this into the expression for the buoyant force:
Fb=d2(Md1)g
- Now substituting Fb back into the equation for Fv:
Fv=Mg−d2(Md1)g
- Factor out g:
Fv=g(M−d2Md1)
- Simplifying gives:
Fv=Mg(1−d2d1)
- Thus, the viscous force acting on the ball is:
Fv=Mg(d1−d2)d1
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct
17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective
16 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A tiny sphere of mass m and density x is dropped in a jar of glycerine of density y. When the sphere aquires terminal velocity, the magnitude of the viscous force acting on it is :
View SolutionTwo copper balls of radius r and 2r are released at rest in a long tube filled with liquid of uniform viscosity. After some time when both the spheres acquire critical velocity (terminal velocity) then ratio of viscous force on the balls is :
View SolutionA small metal ball of diameter 4mm and density 10.5g/cm3 in dropped in glycerine of density 1.5g/cm3. The ball attains a terminal velocity of 8/cms−1. The coefficient of viscosity of glycerine is
View SolutionA small metal ball of diameter 4mm and density 10.5g/cm3 in dropped in glycerine of density 1.5g/cm3. The ball attains a terminal velocity of 8cms−1. The coefficient of viscosity of glycerine is
View SolutionA smooth spherical ball of radius 1cm and density 4×103kg/m3 is dropped gently in a large container containing viscous liquid of density 2×103kg/m3, and η=0.1N−s/m2. The distance moved by the ball in t=0.1sec after it attains terminal velocity is

View SolutionA ball of mass 1 kg is dropped from height 9.8 m, strikes with ground and rebounds at height 4.9 m, if the time of contact between ball and ground is 0.1 s then find impulse and average force acting on ball.
View SolutionA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View SolutionA ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.

View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
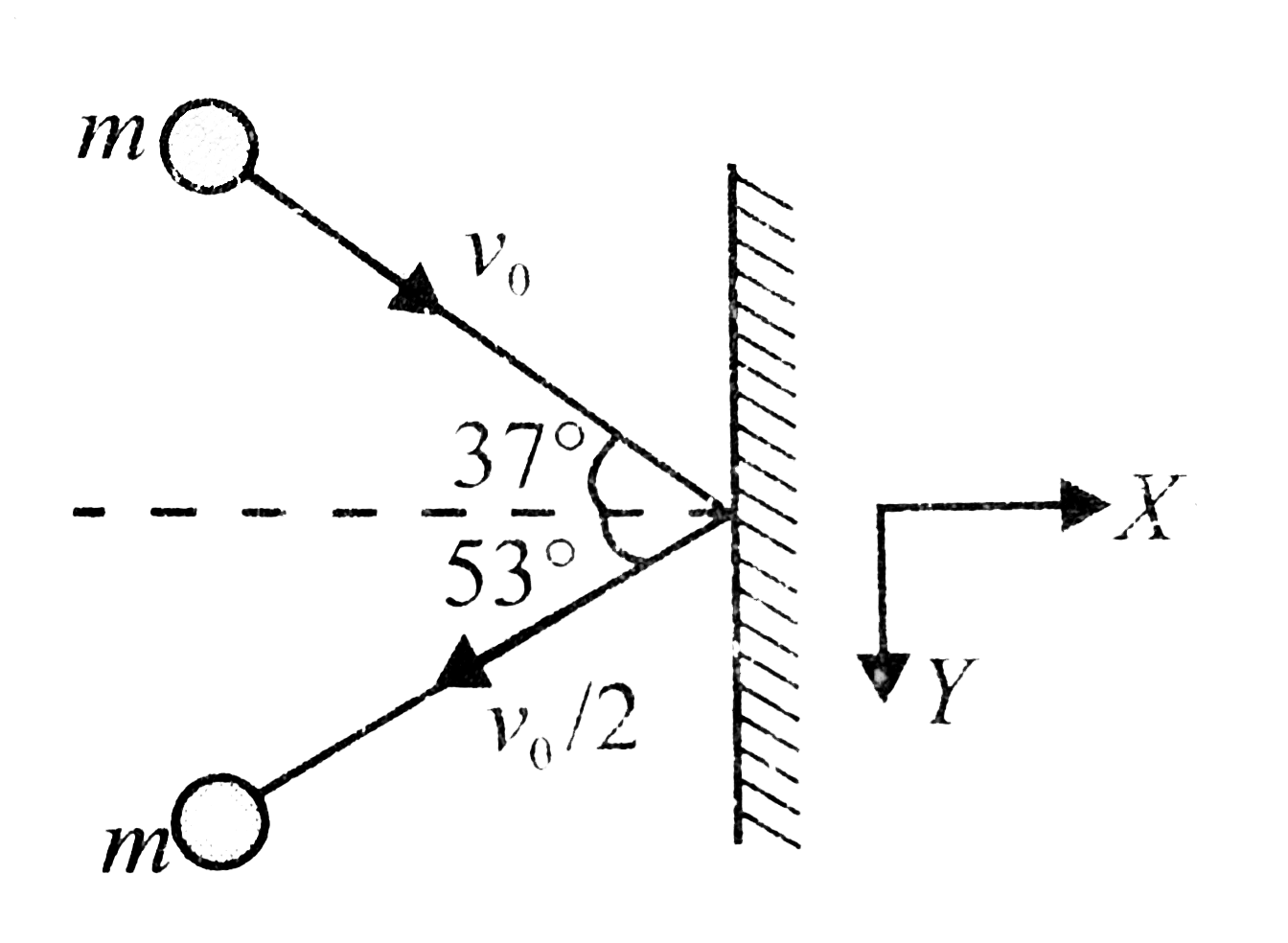
View Solution
