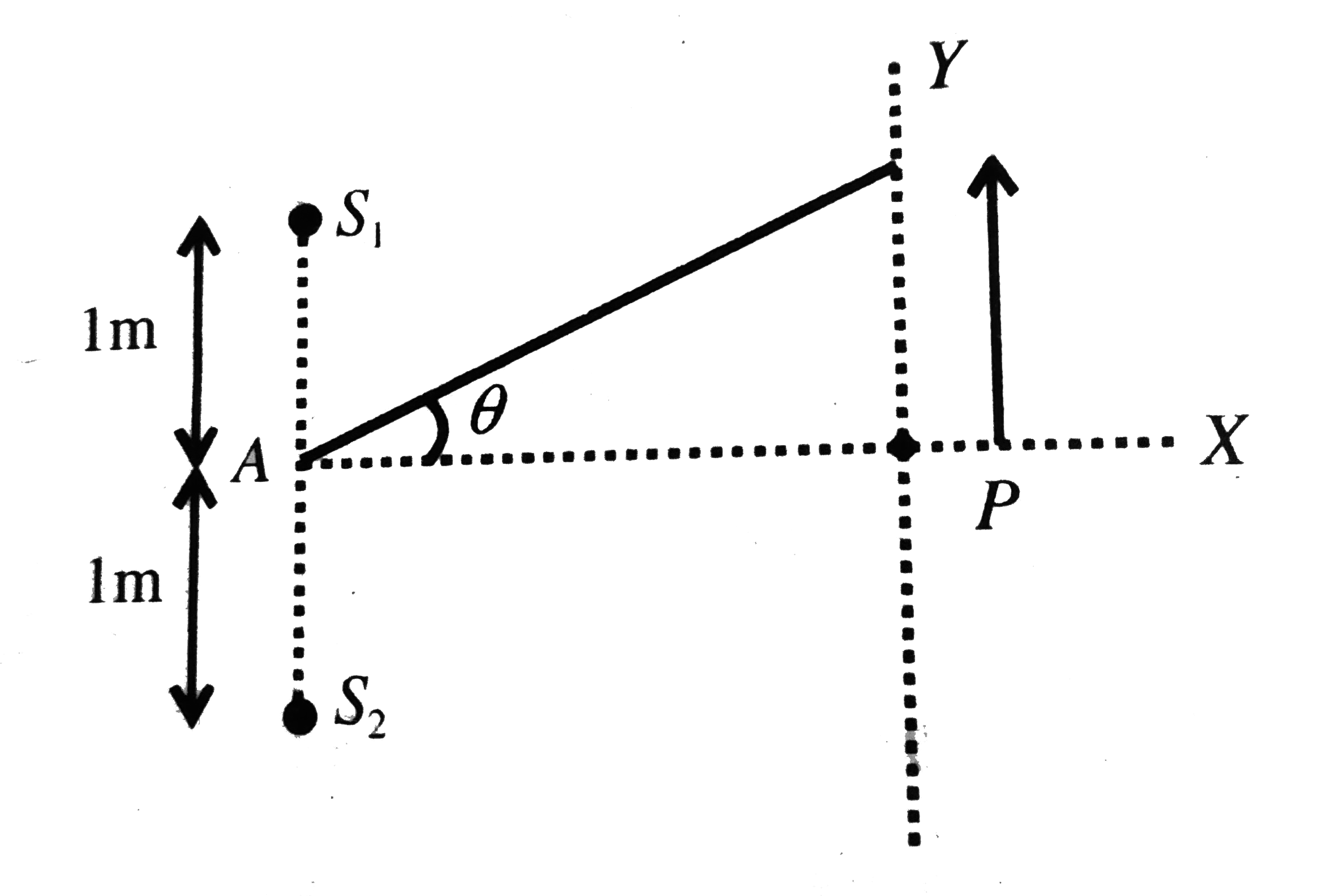
Two speakers derived by the same amplifier and placed at (Fig . 7.9) The speakers vibrate in phase at . A man stands at a point on the x - axis at a very large distance from the origin and starts moving parallel to the Y - axis . The speed of sound in air is .
(a). At what angle will the intensity of sound drop to a minimum for the first time ?
(b) At what angle will the sound intensity be maximum for the first time ?
(c ) If he continues to walk along the line , how many more maxima can he hear ?
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, C
Given
Let OP=D, PQ=y
…..i
Now path difference is given by
where d=2[the proof of x=(yd)/D
a.for minimum intensity
b. for minimum intensity
c. For more maxima
But since the maximum vlaue of theta can be he will hear two more maximum i.e. at .
Topper's Solved these Questions
Similar Questions
A load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
03:55View Solution0.32g of oxygen is kept in a rigid container and is heated. Find the amount of heat needed to raise the temperature from 250C→350C. The molar heat capacity of oxygen at constant volume is 20JK−1mol−1.
05:51View SolutionS1,S2,...,S10 are the speakers in a conference. If S1 addresses only after S2, then the number of ways the speakers addresses is
10:31View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1
 02:31View Solution
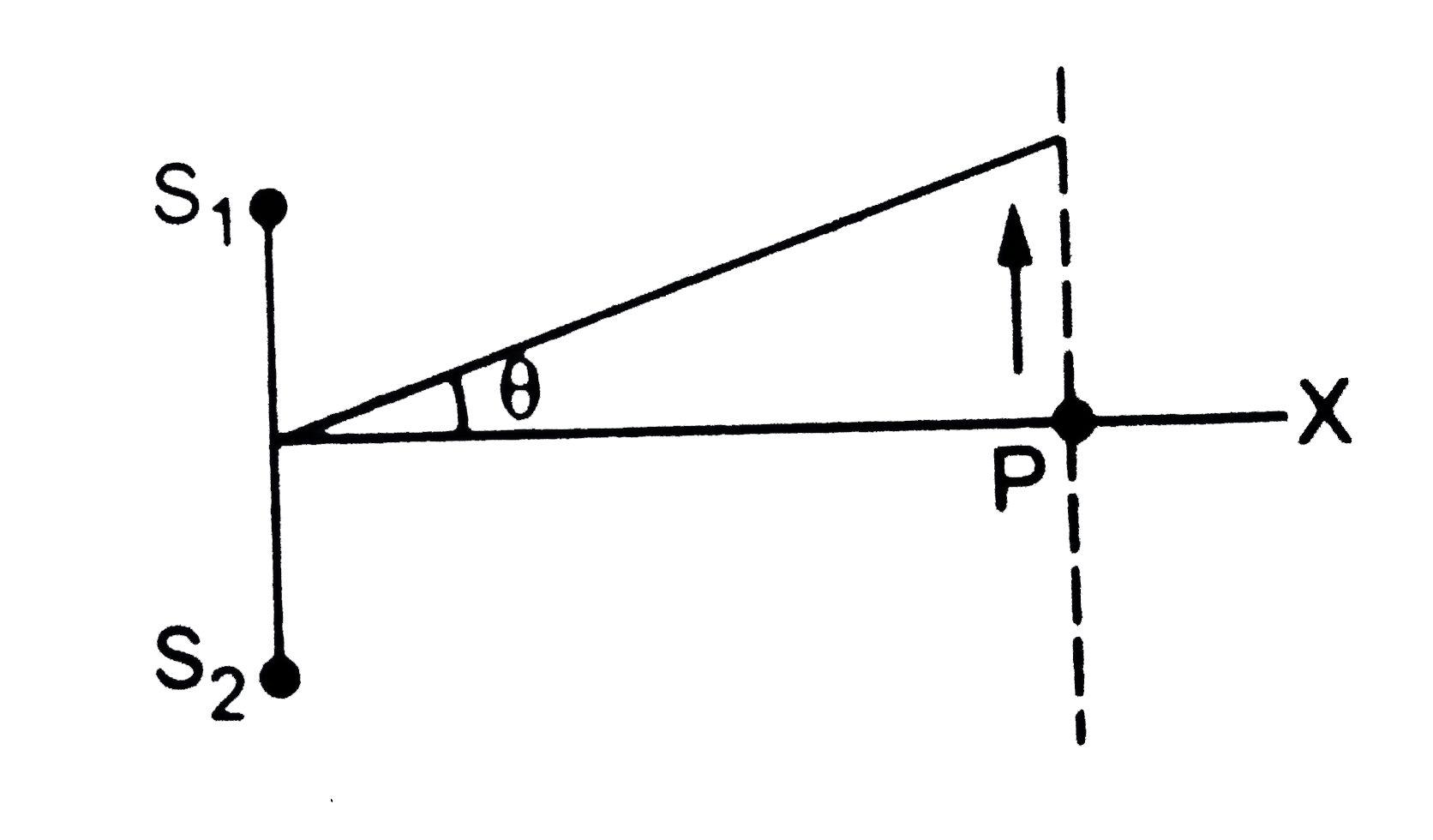
02:31View SolutionTwo speakers S1andS2 , driven by the same amplifier, areplaced at y=1.0mandy=−1.0m. The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is330ms−1 (a) At what angle θ will the intensity of sound drop to a minimum for the first time ? (b) At what angle will he hear a maximum of sound intensity for the first time ? (c) If he continues to walk along the line, how many more maxima can he hear ?
 03:54View Solution
03:54View SolutionTwo sound speakers are driver in phase by an audio amplifier at frequency 600HZ. The speed of sound is 340m/s. The speakers are on the y- axis, one at y=+1.0m and the other at y=−1.0m . A listener begins at y=0 and walks along a line parallel to the y - axis at a very large distance x away.
(a) At what angle θ (between the line from the origin to the listener at the x - axis) will she first hear a minimum sound intensity?
(b) At what angle will she first hear a maximum (afer θ=o∘) sound intensity?
(c ) How many maxima can she possible hear if she keeps walking in the same direction?02:20View SolutionFrom the origin at the same time two points being to move. The first moves on the X-axis at a speed =4 m/s, and the second on the Y axis at a spe3ed of 3 m/ sec.
04:39View Solutiontwo speakers A and B , placed 1 m apart, each produces sound waves of frequnecy 1800 Hz. In phase. A detector moving parallel to line of speakers distant 2.4 m away detects a maximum intensity at O nd then at P. speed of sound wave is
04:16View SolutionA small speaker has a capacity of power 3 W. A microphone is placed at distance 2 m from the speaker. Fine the displacement amplitude of particles of air near to microphone. The frequenct of sound emitted bt speaker is 1.0 KHz (Density of air = 1.2 kg//m^(3) and speed of sound in air = 330 m/s)
10:55View Solutionदो धवनि स्पीकर कुछ दुरी पर रकते हुए है और एक ही विधुत यंत्र द्वारा बजाय जा रहे यह विधुत यंत्र एक निश्चित आवर्ती से स्पीकर को कंपित करा सकता है एक मनुष्य ऐसी जगह बीटा है झा उसकी दुरी एक स्पीकर से 6.0 m तथा दूसरे से 6.4 m है यदि इनके कंपन की आवर्ती को 500 Hz से धीरे धीरे बढ़ाकर 5000 Hz तक ले जाया तो किन किन अवर्तीयो पर उस मनुष्य को विनाशी वियतिकरण का अनुभव होगा में धवनि की चल 320 m/s
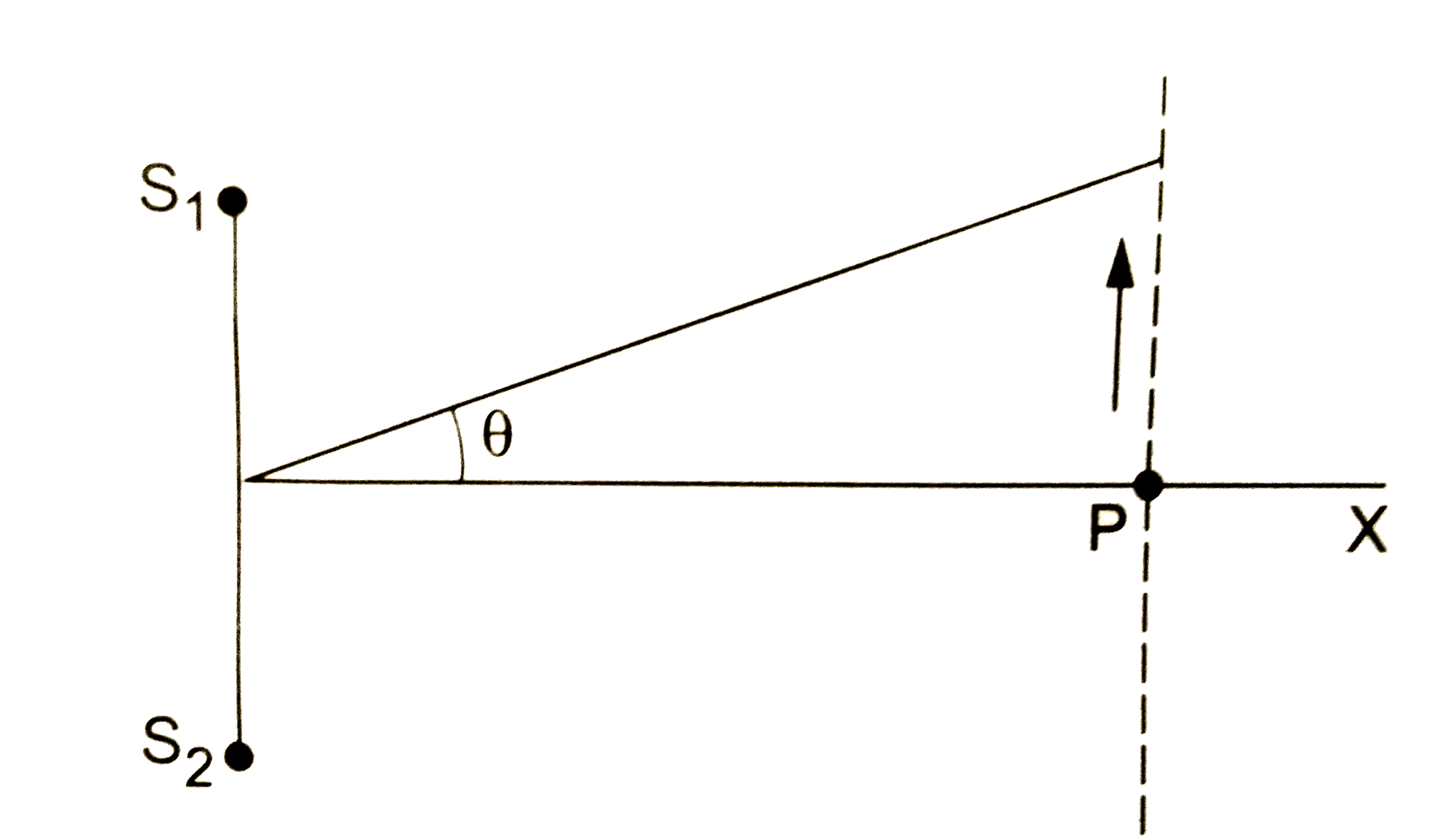
03:29View Solutionएक ही परिपथ से संचालित दो स्पीकर S1 तथा S2y=1.0m तथा y=−1.0m पर रखे गए है स्पीकर 600 Hz की आवर्ती की साथ एक ही कला में कंपन कर रहे है एक मनुष्य अक्ष पर काफी दूर खड़ा है और Y अक्ष के समानांतर चलना प्रारंभ करता है हवा में धवनि की चल 330 m/s है (a) θ के किस मान के लिए पहली बार धवनि की त्रीवता न्यूनतम होगी (b) θ की किस मान की लिए पहले बार धवनि की त्रीवता अधिकतम होगी (c ) यदि वह चलना जारी रखे तो कितनी और बार वह अधिकतम त्रीवता सुनेगा
 03:02View Solution
03:02View SolutionTwo sources S_(1) and S_(2) of sound having frequencies 338, 342 Hz are separated by a large distance. The speed of sound is 340 m/s. The velocity of the observer who is moving from S_(2) " to " S_(1) so that he does not hear any beats is
03:39View SolutionTwo microwave sources S_(1) and S_(2) are located at a distance of 4 lambda from each other along Y-axis,with S_(1) at the origin as shown in the figure.A microwave detector D moves along the X-axis away from S_(1) .The first maximum is obtained for x equal to: (wavelength of the microwave is
05:19View Solutions1,s2 ...............,s10 are the speakers in a conference, If s1 addresses only after s2, then the number of ways the speakers address is
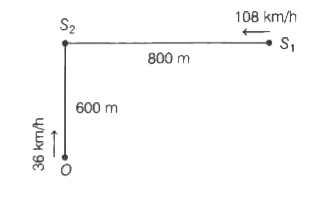
04:08View Solutionएक रेलगाड़ी(S1)108 किमी/घंटा के समान वेग से चलते हुए दूसरी रेलगाड़ी(S2) जोकि स्टेशन पर खड़ी है, कि तरफ जा रही है| एक श्रोता (O)36 किमी/घंटा के समान वेग से S2 की तरफ चित्रानुसार जा रही है| दोनों रेलगाड़ी 120 हर्ट्ज कि समान आवृति कि सीटियाँ बजा रही है| जबO कि दूरीS2 से 600 मी है तथाS1 और S2 के बीच कि दूरी 800 मी है, तब O के द्वारा सुने गए विस्तंदो (Beats) कि शंख्या .......हर्ट्ज है|
[ध्वनि कि गति=330 मी/से ]
 02:50View Solution
02:50View Solutionदो ध्वनि स्त्रोत S1 तथा S2 एक ही आवृत्ति 660 Hz की ध्वनि उत्पन्न करते है। एक श्रोता S1 से S2 की तरफ गति u मी/से से जाते हुए प्रति सेकण्ड 10 विस्पन्द सुनता है। यदि ध्वनि की गति 330 मी/से है, तो u का मान होगा
03:53View Solution

